LWM 2010: Beweis mit Skalarprodukt

Aufgaben 5 vom LWM 2010, Runde 1:

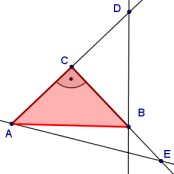
Gegeben ist ein gleichschenklig-rechtwinkliges Dreieck ABC mit dem rechten Winkel bei C. Die Punkte D und E liegen außerhalb des Dreiecks auf den Halbgeraden AC bzw. CB (vgl. Abbildung).
Beweise: Die Strecken CD und CE und sind genau dann gleich lang, wenn sich die Geraden AE und BD rechtwinklig schneiden.

Hinweise zur Animation:

• Beachten Sie, dass der erste Aufruf der Animationen etwas Zeit in Anspruch nimmt. (Sie benötigen zur Anzeige Java 1.4.2 oder höher.)
• Die Animation lässt sich mit dem hellblauen Pfeilsymbol (oben rechts) in den Anfangszustand zurück setzten.
• Bei beiden Beweisrichtungen müssen die Vektoren DB und AE durch die Basisvektoren beschrieben werden. Mit Hilfe der Voraussetzung wird anschließend die Behauptung bewiesen.
• Ein ausführlicher Lösungsvorschlag zum Download befindet sich am Seitenende.
• Weitere Beweisaufgaben mit Vektoren finden Sie hier: hier.

Lösungsvorschlag:

Vergrößern

Dokument-Download als OpenOffice- und als PDF-Datei

Dokument als OpenOffice-Datei Download
Dokument als PDF Download