Verschiebung der Normalparabel in y-Richtung

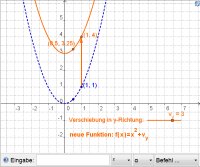In der nachfolgenden Animation kannst Du herausfinden, wie sich eine Verschiebung der Normalparabel in y-Richtung auf den zugehörigen Funktionsterm der Quadratfunktion auswirkt.

Hinweise zur Animation:

• Beachte, dass der erste Aufruf der Animationen etwas Zeit in Anspruch nimmt.
• Bei Problemen informiere bitte die Redaktion Mathematik.
• Die Animation lässt sich mit dem Pfeilsymbol (oben rechts) in den Anfangszustand zurück setzten.

Aufgaben

1. Verändere den Schieberegler für den Verschiebungswert in y-Richtung.
2. Wie lassen sich die orangenen Punkte aus den Koordinaten der entsprechenden blauen Punkte berechnen?
3. Formuliere einen Merksatz im Heft, aus dem hervorgeht, wie man die Quadratfunktion bei einer Verschiebung der Normalparabel in y-Richtung anpassen muss.
4. Wie wirkt sich eine negative Verschiebung in y-Richtung auf das Schaubild aus?
5. Beachte die Unterschiede zur Verschiebung in x-Richtung.