LWM 2010, Aufgabe 5: Streckengleichheit und Orthogonalität

Aufgabenstellung

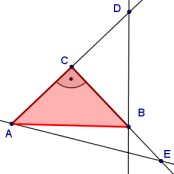
Gegeben ist ein gleichschenklig-rechtwinkliges Dreieck ABC mit dem rechten Winkel bei C. Die Punkte D und E liegen außerhalb des Dreiecks auf den Halbgeraden AC bzw. CB (vgl. Abbildung).
Beweise: Die Strecken CD und CE und sind genau dann gleich lang, wenn sich die Geraden AE und BD rechtwinklig schneiden.

Hinweise

• Beachte die Wörter "genau dann" und ihre Bedeutung.
• Nachmessen in einer Konstruktion ist kein Beweismittel.
• Im Folgenden werden drei Beweisvarianten beschrieben, wobei für die dritte Variante das Skalarprodukt aus der Vektorgeometrie (Jahrgangsstufe) zu Hilfe genommen wird.
• Die anderen Aufgaben des Wettbewerbs mit Lösungen findest du unter www.landeswettbewerb-mathematik.de.

Beweis mit Kongruenz und Winkelgleichheit (Ähnlichkeit)

Für diese Beweisvariante wird die Kenntnis der Kongruenzsätze vorausgesetzt. Neben einer Animation stellen wir ein Arbeitsblatt mit "Beweislücken" und zugehörigem Lösungsblatt vor.

Zum Beweis: Beweis mit Kongruenz.

Beweis mit Höhenschnittpunkt im Dreieck

Diese Variante ermöglicht die Vernetzung des Satzes vom Höhenschnittpunkt mit den Kongruenzsätzen. Hierbei verändert eine zusätzliche Linie die Skizze. Auch in diesem Fall werden Kongruenzsätze benötigt.

Zum Beweis: Beweis mit Höhenschnittpunkt.