Aufgabe 2, Landeswettbewerb Mathematik 2013 (Runde 2)
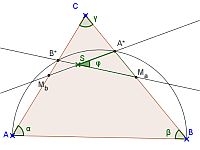
Im abgebildeten Dreieck ABC sind Ma und Mb Seitenmittelpunkte. Das Dreieck wurde dabei so gewählt, dass der Halbkreis über [AB] die anderen Seiten zwischen Ma und C sowie zwischen Mb und C in den Punkten A* bzw. B* schneidet.
Bestimme in diesem Dreieck den Schnittwinkel der Geraden MbA* und MaB* in Abhängigkeit von den Innenwinkeln des Dreiecks ABC.
Zum Verständnis des animierten Beweises solltest du neben den grundlegenden mathematischen Sätzen über Basiswinkel im gleichschenkligen Dreieck und die Winkelsumme im Dreieck auch den Umfangswinkelsatz (=Peripheriewinkelsatz) und den Umfangswinkel-Mittelpunktswinkelsatz kennen.
Hinweise zur Animation
- Durch Verschieben der Punkte A, B oder C lässt sich die Form und Lage des Dreiecks verändern. Beachte hierbei die Vorgabe für die Position von C in der Aufgabenstellung.
- Wenn du die Schalter oben links nacheinander in den grünen Bereich schiebst erhältst du schrittweise Hinweise zur Lösung.
- Mit dem blauen Pfeilsymbol am rechten oberen Rand kannst du die Animation in den Anfangszustand zurück setzen.


