Der Inkreis im Höhenfußpunktdreieck
Verbindet man bei einem Dreieck die Schnittpunkte der Dreieckshöhen (Höhenfußpunkte), so entsteht das so genannte Höhenfußpunktdreieck. Eine bemerkenswerte Eigenschaft des Höhenfußpunktdreiecks wollen wir im Folgenden beweisen:
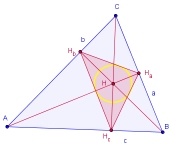
Beweise:
Der Schnittpunkt der Dreieckshöhen ist bei einem spitzwinkligen Dreieck gleichzeitig der Mittelpunkt des Inkreises vom zugehörigen Höhenfußpunktdreieck.
Hinweise:
- In der Konstruktion lassen sich die Dreiecksecken verschieben.
- Mit dem hellblauen Pfeilsymbol oben rechts auf dem Zeichenblatt kannst du die Konstruktion zurück setzten.
- Beachte, dass der Satz nur für spitzwinklige Dreiecke gültig ist (vgl. Zusatzfrage).
- Für den Beweis musst du die Eigenschaften des Inkreismittelpunktes kennen. Außerdem sollte neben dem Satz über die Winkelsumme der Innenwinkel beim Dreiecke auch der Thaleskreis, sowie die Aussage des Umfangswinkelsatzes bekannt sein.
(Alternativ-Beweise werden von der Mathematik-Redaktion gerne angenommen und veröffentlicht.)
Aufgaben:
- Wiederhole die Beweisführung für die anderen beiden Innenwinkel. Fasse die Vorgehensweise stichwortartig zusammen.
- Konstruiere den Inkreis des Höhenfußpunktdreiecks zunächst dynamisch in der nachfolgenden GeoGebra-Datei und anschließend mit Zirkel und Lineal im Heft. Erinnere dich, dass der Inkreis in der Regel die Schnittpunkte der Winkelhalbierenden mit den Seiten nicht berührt.
Tipp: Benutzte bei der dynamischen Konstruktion für den Inkreis das Werkzeug "Kreis mit Mittelpunkt durch Punkt" und konstruiere damit drei (identische) Inkreise - dann sollte der Kreis auch bei stumpfwinkligen Dreiecken bestehen bleiben.
Zusatzfragen für Spezialisten:
- Welche Beziehung zum roten Dreieck hat der ursprüngliche Inkreis bei stumpfwinkligen Dreiecken?
- Warum verschwindet der Kreis beim stumpfwinkligen Dreieck, wenn man bei der (dynamischen) Konstruktion das Werkzeug "Kreis durch drei Punkte" verwendet?



