Beweisen gehört zur hohen Kunst der Mathematik. Sie lässt sich mit ein wenig Übung und der Kenntnis einiger grundlegender geometrischer Sätze erlernen.
Im Folgenden werden Beweise zu verschiedenen mathematischen Aussagen mit Hilfe von Animationen skizziert.
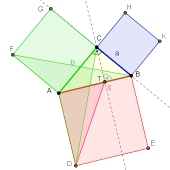
Beweisvarianten zum Satz des Pythagoras
Der Satz des Pythagoras ist sicherlich der bekannteste aller mathematischen Sätze. Er wurde auf unzählige Arten bewiesen. Unter folgendem Link findest du eine Auswahl der interessantesten Beweise zum Teil mit Animationen.
Animierte Beweisvarianten vom Satz des Pythagoras
Kongruenzbeweise
Mit Hilfe der Kongruenzsätze lassen sich viele geometrische Zusammenhänge begründen. Sie sind wertvolle Werkzeuge zum Nachweis gleicher Längen oder bei der Begründung von Flächengleichheiten in Dreiecken. In dieser Lernumgebung findest Du Erklärungen und Beispiele.
Lernumgebung zu Kongruenz mit Übungsaufgaben
Rückwärts Rechnen als Beweistechnik
In vielen Fällen kann man beim Beweisen schon zu Beginn einen Zusammenhang, den es zu begründen gilt. Durch geschickte Umformungen gelangt man in manchen Fällen vom eigentlichen Ziel des Beweises zur Ausgangssituation. Beispiele zu Beweisführungen durch Rückwärtsrechnen findest Du unter dem folgenden Link.
Lernumgebung: Rückwärts Rechnen als Beweistechnik
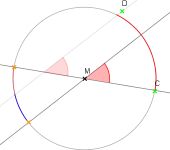
Der Umfangswinkelsatz
Der Umfangswinkelsatz zählt du den wichtigsten Sätzen in der Mathematik. Leider wird er in der Schulmathematik nur sehr selten vermittelt. Er lässt sich sehr leicht beweisen und beinhaltet verschiedene geometrische Zusammenhänge. So folgt aus dem Umfangswinkelsatz als Spezialfall beispielsweise der Satz des Thales und weiter liefert er vielfältige Erkenntnisse über Winkelbeziehungen am Dreieck und zwischen verschiedenen Dreiecken. Der hier vorgestellte sehr anschauliche Beweis benötigt kaum geometrische Vorkenntnisse und vermittelt auf einfache Weise eindrucksvoll den Zusammenhang zwischen Mittelpunktswinkel und Umfangswinkel.
Lernumgebung mit Beweis und Aufgaben zum Umfangswinkelsatz
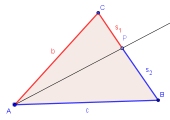
Der Satz von der Winkelhalbierenden
Die Winkelhalbierende teilt die gegenüber liegende Seite im Verhältnis der Längen ihrer anliegenden Seiten. Hier findest du einen eleganten Beweis dieser Aussage.
Bei dem interaktiven Beweis des Satzes kannst du dir bei Bedarf mehrere Tipps und Teilkonstruktionen anzeigen lassen. Der Beweis ist eine schöne Anwendung des ersten Strahlensatzes, der mit einem Trick angewendet werden kann. Allerdings muss nachgewiesen werden, dass die Voraussetzungen für den Satz erfüllt sind.
Der Satz von der Winkelhalbierenden mit animiertem Beweis
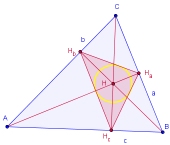
Der Inkreis im Höhenfußpunktdreieck
Bildet man aus den drei Höhenfußpunkten eines Dreiecks ein "inneres" Dreieck, so lassen sich zum Inkreis dieses so genannten Höhenfußpunktdreiecks weitere interessante Aussagen bilden:
Der Inkreismittelpunkt im Höhenfußpunktdreieck ist bei einem spitzwinkligen Dreieck gleichzeitig der Schnittpunkt der Dreieckshöhen. Der Beweis dieses Satzes verbindet elementare geometrische Aussagen (Winkelsumme im Dreieck, Thalessatz und Umfangswinkelsatz) und stärkt somit in hohem Maße das vernetzte Denken. Darüber hinaus liefert die dynamische Animation weitere interessante Zusammenhänge zwischen dem Höhenfußpunktdreieck und dem Ausgangsdreieck insbesondere bei stumpfwinkligen Dreiecken.
Der Inkreis im Höhenfußpunktdreieck - Eigenschaften mit Begründungen
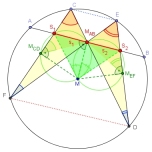
Das Schmetterlings-Theorem
Die hier vorgestellte Konstruktion zeigt eine offensichtliche Ähnlichkeit zu einem Schmetterling. Der Nachweis der Längengleichheit der entsprechenden Seiten in der Konstruktion wird hier mit einer Animation in mehreren Schritten angedeutet.
Das Schmetterlings-Theorem mit animiertem Beweis
Der Satz des Ptolemäus und seine Umkehrung

Im Gegensatz zum Ptolemäischen Weltbild hat der Satz des Ptolemäus bis heute seine Gültigkeit. Leider ist er inzwischen weitgehend in Vergessenheit geraten. Auf den folgenden Seiten wird dieser schöne Satz mit seiner Umkehrung vorgestellt. Darüber hinaus beschreiben dynamische GeoGebra-Animationen mit Schiebeschaltern die Struktur eines möglichen Beweises. Auch werden Anwendungen des Satzes von Ptolemäus am Beispiel des Satzes von Pythagoras und dem Kosinussatz vorgestellt. Voraussetzungen für das Verständnis sind die Kenntnis des Umfangswinkelsatzes sowie den Eigenschaften von zentrischen Streckungen. Beim Beweis des Kosinussatzes wird darüber hinaus die Definitionserweiterung auf beliebige Winkel beim Kosinus vorausgesetzt.
Lernumgebung zum Satz des Ptolemäus und seiner Umkehrung
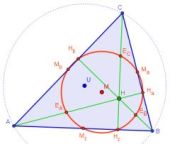
Der Feuerbachsche Kreis (auch 9-Punkte-Kreis
Der Feuerbachsche Kreis liefert sicherlich einen der schönsten geometrischen Zusammenhänge überhaupt. Mit ihm lassen sich völlig verschiedene Dreiecksobjekte in Beziehung bringen. Wir begründen diese Zusammenhänge auf zwei unterschiedliche Arten. Dynamische GeoGebra-Konstruktionen veranschaulichen die Vorgehensweise beim Beweisen spielerisch.
Diese Inhalte richten sich an ambitionierte Mathematiker ab der gymnasialen Mittelstufe und eignen sich nicht nur zu Vorbereitung auf Wettbewerbe sondern auch zur Vernetzung von bekanntem Wissen der Sekundarstufe 1.
Beim ersten Beweis wird lediglich etwas Wissen über die Eigenschaften von Seitenmittenparallelen, Sehnenvierecken und der Mittelparallelen eines Parallelenstreifens vorausgesetzt. Beim Alternativbeweis kommt noch die Umkehrung des Thalessatzes hinzu. Schließlich liefert die Anwendung der zentrischen Streckung einen überraschenden Zusammenhang zwischen Feuerbachkreis und Umkreis.
Zusätzlich steht eine Zusammenfassung beider Beweise mit weiteren Hinweisen zum Download bereit.
Lernumgebung zu den Zusammenhängen am Feuerbachschen Kreis (9-Punkte-Kreis)
Beweisaufgabe mit Sehnenvierecken und Umfangswinkelsatz
Bei dieser Übungsaufgabe zum Umfangswinkelsatz (auch Peripheriewinkelsatz oder Randwinkelsatz) muss die Richtigkeit einer interessanten Höhenkonstruktion beim Dreieck nachgewiesen werden. Für das Verständnis des Beweises wird neben dem Umfangswinkelsatz auch die Kenntnis der Winkeleigenschaft von Sehnenvierecken vorausgesetzt. Die animierte Aufgabe ist neben dem Unterrichtseinsatz sehr gut zum Selbststudium bei der Vorbereitung auf Wettbewerbe geeignet.
Beweisaufgabe mit Sehnenvierecken und Umfangswinkelsatz
Nachweis gleicher Winkel - mit Lernvideo und Animation
Mit Hilfe des Umkreises und einem "Berührkreis" an eine Dreiecksseite wird ein Winkel halbiert. Dies soll in einem Beweis begründet werden. Im Beweis werden Umfangswinkel, Sehnen-Tangenten-Winkel, gleichschenklige Dreiecke und Stufenwinkel an Parallelen verwendet. Anhand der Aufgabe werden verschiedene nicht triviale "Werkzeuge" zum Nachweis von Winkelgleichheit vorgestellt.
Mit Hilfe einer Animation und eines Lernvideos werden die einzelnen Beweisschritte dargestellt und erläutert. Weitere Aufgaben und Fragestellungen ergänzen das Angebot. Das Lernvideo geht neben dem Beweis näher auf den Zusammenhang zwischen Umfangswinkel und Sehnen-Tangenten-Winkel ein.
Nachweis gleicher Winkel - mit Lernvideo und Animation
Nachweis gleicher Längen - verschiedene Aufgaben mit Animationen
Wir präsentieren dir zwei Beweisvorschläge zu Wettbewerbsaufgaben aus dem Landeswettbewerb Mathematik zum Nachweis gleicher Längen.
Im ersten Beweis wird die Aufgabe mit Hilfe einer Streifenschar gelöst.
Der zweite Beweis verwendet die beiden Kongruenzabbildungen Spiegelung und Drehung und führt damit die Längen ineinander über. Hierzu bieten wir dir auch ein passendes Lernvideo.
Wettbewerbsaufgaben mit Nachweis gleicher Längen
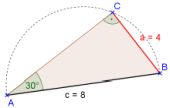
Aufgabe aus Mathematik ohne Grenzen mit wertvollem Hilfssatz
Anhand einer Aufgabe aus einem Probewettbewerb von Mathematik ohne Grenzen wird auf eine einprägsame Besonderheit des rechtwinkligen 30°-Dreiecks hingewiesen. Der Beweis hierzu verlangt einfache geometrische Grundkenntnisse zu gleichschenkligen bzw. gleichseitigen Dreiecken sowie den Mittelparallelen beim Dreieck. Für die Besonderheit des rechtwinkligen 30°-Dreiecks gibt jedoch auch eine ganz einfache Begründung.
Aufgabe aus Mathematik ohne Grenzen mit wertvollem Hilfssatz
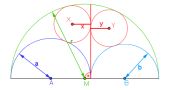
Die Zwillingskreise des Archimedes
Der Nachweis der gleichen Radien bei den Zwillingskreisen des Archimedes ist eine schöne Anwendung des Satzes von Pythagoras unter Verwendung der binomischen Formeln. Schieberegler in der zugehörigen Animation erleichtern das Verständnis der Beweisstruktur.
Die Zwillingskreise des Archimedes
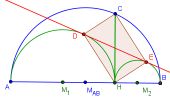
Vier Punkte auf einer Kreiskonstruktion beschreiben ein Rechteck
Mit einer ähnlichen Halbkreis-Konstruktion, wie bei den den Zwillingskreisen des Archimedes, erhält man mit Hilfe einer geeigneten Tangenten vier Punkte auf den Kreisen, die offensichtlich ein Rechteck beschreiben.
Vier Punkte auf einer Kreiskonstruktion beschreiben ein Rechteck



