Zurück

Nachweis gleicher Längen - mit Drehung und Spiegelung

Skizze zur Aufgabenstellung

Aufgabenstellung

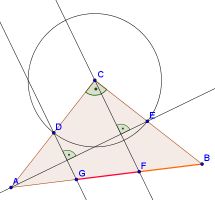
Im gleichschenklig Rechtwinkligen Dreieck ABC mit dem rechten Winkel bei C schneidet ein Kreis um C die Kathete CB in einem Punkt E sowie die Kathete CA in einem Punkt D. Die beiden Senkrechten von C und D auf die Gerade AE schneiden die Hypotenuse AB in den Punkten F und G.
Zeige, dass die Strecken GF und FB gleich lang sind.

Hinweise zur Animation:

  • In der Konstruktion kannst du die Basis des Dreiecks ABC sowie der Radius des Kreises verändern.
  • Mit dem Pfeilsymbol oben rechts auf dem Zeichenblatt kannst du die Konstruktion zurück setzten.

Aufgaben:

  1. Gib die zentralen Beweisschritte in eigenen Worten wieder.
  2. Bei "Trick" wird der Kongruenzsatz sws gar nicht verwendet. Weise die Streckengleichheit ohne den Kongruenzsatz sws (nur mit der Drehung) nach.