Nachweis: Vier Punkte beschreiben ein Rechteck

Aufgabe 4 Landeswettbewerb-Mathematik (LWM) aus dem Jahr 1989 (Runde 2)

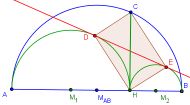Skizze Auf einem Halbkreis über AB wird ein Punkt C beliebig gewählt. Die Senkrechte zu AB durch C schneidet AB in H. Über AH und HB werden erneut Halbkreise gezeichnet.
Die gemeinsame Tangente berührt die beiden Halbkreise in den Punkten D und E.

Zeige: Das Viereck CDHE ist ein Rechteck.

Tipps zur Beweisführung:

  • Unterhalb dieses Textes findest Du eine Animation zur Beweisführung. (Der erste Start kann etwas dauern.) Die zughörige Beweisskizze wird durch Öffnen der ersten drei Schiebeschalter schrittweise angezeigt. Mit dem dritten Schalter erscheinen alle Objekte auf einmal.
  • Es genügt, wenn wir die Fälle betrachten, bei denen der Punkt C (und damit auch H) näher an B als an A liegt. (Im umgekehrten Fall spiegelt man die Anordnung an der Mittelsenkrechten von AB und vertauscht die Bezeichnung für A und B.)
  • Beachte, dass die Radien der der drei Kreise von einander abhängen. Formuliere eine Beziehung zwischen r, r1 und r2.
  • Im vorgestellten Beweis steht die Anwendung des Satzes von Pythagoras als Kongruenznachweis im Vordergrund. Hierfür muss man zunächst einen Trick anwenden. Welchen? Auch die Gleichheit der Tangentenabschnitte von einem Punkt außeralb eines Kreises ist ein einfaches Beweismittel. Neben dem hier vorgestellten Lösungsweg gibt es noch weitere.
  • Erstelle möglichst eine eigene Lösung. Wenn du der Beweisführung folgst, fasse die wesentlichen Schritte in eigenen Worten in einem Heftaufschrieb zusammen. Erkläre den Beweis einem Freund / einer Freundin.
  • Vergleiche Aussage der Aufgabenstellung mit den "Zwillingskreisen des Archimedes". Hier erhält man durch die beiden inneren Kreise kein Rechteck, sondern zwei kongruente Kreise. Auch dies lässt sich mit dem Satz des Pythagoras nachweisen.

Beachte:

  1. Bei einer sauberen Beweisführung müssen alle wesentlichen Zwischenschritte aufgeführt werden.
  2. Insbesondere müssen alle verwendeten mathematischen Sätze, die aus dem Unterricht (oder dem Schulbuch) nicht bekannt sind, präzise formuliert und mit einem Quellennachweis (z. B. Formelsammlung oder Internetseite) belegt werden.
  3. Wenn Du einen Satz verwendest, überprüfe immer, ob die Voraussetzungen für den Satz gegeben sind. Beim Satz des Pythagoras muss beispielsweise ein rechtwinkliges Dreieck zu Grunde liegen (Nachweis!).