Rückwärts Rechnen
Rückwärts rechnen zählt zu den wichtigsten Beweistechniken bei elementargeometrischen Problemen. Hiermit lassen sich viele Beweisaufgaben elegant und auf natürliche Weise lösen. Nachfolgend wird die Beweistechnik des Rückwärts Rechnens an verschiedenen Beispielen vorgestellt.
Herzlichen Dank an dieser Stelle an Christian Messner aus Singen für die vielen tollen Materialien.
Vorgehensweise beim Rückwärts Rechnen.
Man beginnt bei dieser Technik mit der Behauptung des Satzes und versucht Schritt für Schritt, (unter Umständen mit Hilfe von Hilfslinien, Spiegelungen, Drehungen) die Aussage auf die Voraussetzungen des Satzes zurückzuführen. Hierfür verwendet man bekannte mathematische Sätze.
Schwierigkeiten:
- Wie weise ich gleiche Längen nach?
- Wie weise ich gleiche Winkel nach?
- Wie weise ich die Gleichheit von Figuren nach?
Mögliche Hilfen:
- Auflistung wichtiger mathematischer Sätze (siehe "Begründungsbasis von Gerhard Schneider"?
 Vergrößern
Vergrößern
Dokument-Download:
Dokument als OpenOffice-Datei: Download
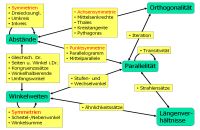
Dokument als PDF-Datei: Download - "Beweislandkarte" von Christian Messner mit Zielen und zugehörigen Beweismitteln
-
Dokument-Download:
Dokument als OpenOffice-Datei: Download
Dokument als PDF-Datei: Download
Beispiele:
Anhand der folgenden Beispiele wird die Strategie beim Rückwärts Rechnen schrittweise vorgeführt. Zu jedem Beispiel gibt es darüberhinaus eine Animation.
- Beispiel 1: Winkelbestimmung mit gleichschenkligen Dreiecken und Wechselwinkelsatz.
- Beispiel 2: Der Satz von der Winkelhalbierenden im Dreieck - zum Beweis werden die Strahlensätze benötigt.
- Beispiel 3: Der Satz des Thales - hier verwenden wir unsere Kenntnisse über den Umkreis bei Dreiecken, sowie die Eigenschaften der Mittelparallelen eines Streifens.