Zurück

Schritt 3 (Anwendung der Strahlensätze)

Der zweite Strahlensatz ist in unserem Fall gleich zwei Mal eine gute Wahl.

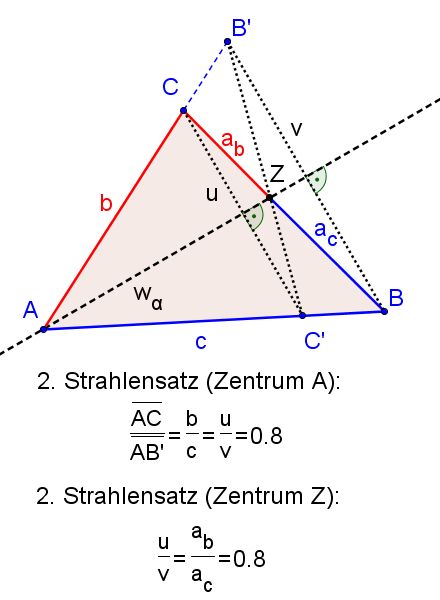
Zunächst einmal liegen die Strecken der Dreiecksseiten b und c beide auf den Schenkeln unserer achsensymmetrischen Figur. Darüber hinaus sind die Strecken u und v parallel.

Somit gilt zunächst mit dem Zentrum A: Verhälntis b/c

Betrachte nun das Zentrum Z. Hier gilt die Verhälnisgleichung Verhälntis ab/ac

 

Insgesamt erhalten wir hieraus die Behauptung: Verhälntis b/c

Skizze

Hinweis

Einen weiteren animierten Beweis zu unserer Behauptung über die Winkelhalbierende im Dreieck (mit dem ersten Strahlensatz) findest du hier. Vergleiche die Vorgehensweise bei beiden Beweisen.