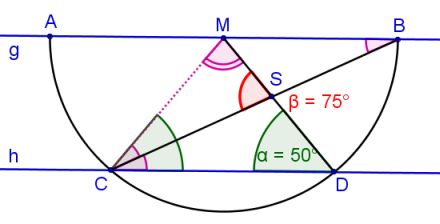
Schritt 3 (Wechselwinkel an Parallelen):
Der Winkel ![]() bei B taucht bei C zweimal auf. Der untere stimmt aufgrund der Gleichheit von Wechselwinklen an Parallelen mit den Basiswinkeln des Dreiecks CBM überein.
bei B taucht bei C zweimal auf. Der untere stimmt aufgrund der Gleichheit von Wechselwinklen an Parallelen mit den Basiswinkeln des Dreiecks CBM überein.
![]() teilt somit
teilt somit ![]() genau in der Mitte.
genau in der Mitte.
D. h. ![]() = 25°.
= 25°.
Insgesamt folgt aus ![]() +
+![]() +
+![]() =180° unser Ergebnis:
=180° unser Ergebnis: ![]() =180°-25°-80°=75°.
=180°-25°-80°=75°.