Besondere Schnittpunkte im Dreieck
In der Ebene schneiden sich zwei nicht parallele Geraden immer. Schneiden sich drei Geraden in einem Punkt, so ist das immer eine Besonderheit, die es zu begründen gilt.
In der Schulmathematik lernen wir als Schnittpunkte den Umkreismittelpunkt, den Inkreismittelpunkt, den Schwerpunkt und evtl. auch noch den Höhenschnittpunkt kennen. Es gibt jedoch eine ganze Menge mehr von diesen Schnittpunkten (siehe "Besondere Punkte im Dreieck").
Die Schnittpunkteigenschaften möchten wir an dieser Stelle gerne zu einigen dieser Punkte begründen. Hierfür bieten wir dynamische Animation mit Schiebereglern, die die Beweisstruktur schrittweise offen legen.
In diesem Zusammenhang sei auch der Satz von Ceva erwähnt, der einen Zusammenhang zwischen dem Schnittpunkt und den zugehörigen Streckenabschnitten herstellt.
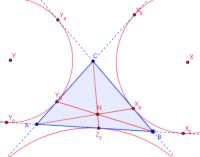
Der Nagelpunkt
Beim Nagelpunkt handelt es sich um den Schnittpunkt der Verbindungsstrecken zwischen Ecken und gegenüberliegenden Ankreisberührpunkten.
Für den Beweis der Schnittpunkteigenschaft wird nach etwas Vorarbeit der Satz von Ceva verwendet. Eine Beweis-Animation führt dich schrittweise zum Ziel.
Die Vorgehensweise dieses Beweises lässt sich leicht übertragen, denn auf die gleiche Art und Weise lässt sich z. B. auch der Schwerpunkt als Schnittpunkt der Seitenhalbierenden, oder der Inkreismittelpunkt als Schnittpunkt der Winkelhalbierenden "überführen".
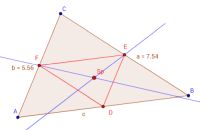
Der Spiekerpunkt als Schwerpunkt des Dreiecksumfangs
Stellt man sich ein Dreieck als "Drahtgestänge" (ohne Inhalt) vor, dann ist der physikalische Schwerpunkt nicht der Schnittpunkt der Seitenhalbierenden, sondern der Schnittpunkt der so genannten Schwerelinien.
Beim Begründen dieses Sachverhaltes stößt man auf weitere Eigenschaften des Spiekerpunktes. So liegen beispielsweise Spiekerpunkt, Schwerpunkt und Inkreismittelpunkt auf einer Linie, wobei der Schwerpunkt die Strecke zwischen Inkreismittelpunkt und Spiekerpunkt im Verhältnis 2:1 teilt. Weitere Eigenschaften und Zusammenhänge z. B. zwischen Spiekerpunkt und Nagelpunkt findest du unter nachfolgendem Link.



