Pyramiden
1 Wichtige Begriffe
1.1 Pyramidenarten: Schiefe- , gerade- und regelmäßige Pyramiden
Man unterscheidet Pyramiden nach der Art ihrer Grundfläche und der Lage ihrer Spitze.
Die Grundfläche einer Pyramide ist ein beliebiges oder regelmäßiges Vieleck mit mindestens 3 Ecken.
Zur Vereinfachung werden Pyramiden häufig nur nach der Anzahl der Seiten ihrer Grundfläche benannt.
Bei einer dreiseitigen Pyramide mit der Seitenzahl n = 3 unterscheidet man:
1.1.1 Schiefe dreiseitige Pyramiden
Die Grundfläche ist ein beliebiges Dreieck. Die Spitze der Pyramide liegt nicht senkrecht über dem Mittelpunkt der Grundfläche. Nicht alle Seitenkanten sind gleich lang. Die Mantelfläche besteht aus drei unterschiedlichen Dreiecken.
1.1.2 Gerade dreiseitige Pyramiden
Die Grundfläche ist ein beliebiges Dreieck. Die Spitze der Pyramide liegt senkrecht über dem Mittelpunkt (Schwerpunkt) der Grundfläche. Alle Seitenkanten sind gleich lang. Die Mantelfläche besteht aus drei gleichschenkligen Dreiecken.
1.1.3 Regelmäßige dreiseitige Pyramide
Die Grundfläche ist ein gleichseitiges Dreieck.
Besteht die Grundfläche aus einem regelmäßigen Vieleck (siehe Abb. 2), sind alle Seitenkanten gleich lang. Die Mantelfläche besteht dann aus n kongruenten gleichschenkligen Dreiecken. Der Einfachheit halber nennen wir regelmäßig Pyramiden nach der Anzahl ihrer Ecken Dreieckspyramide, Fünfeckspyramide, ....usw.
Beispiele für regelmäßige (reguläre) Pyramiden
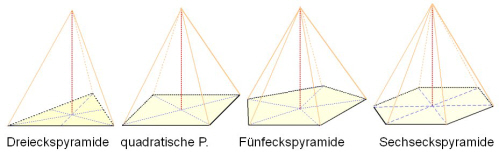
Abb. 2
1.2 Bezeichnungen von Flächen, Kanten und Hilfslinien an Pyramiden
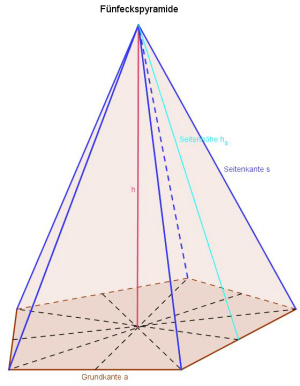 |
|
Ein Beispiel für die Bezeichnungen einer quadratischen Pyramide findet man hier.
2. Berechnungen an Pyramiden
Wichtige Voraussetzung für Berechnungen an Pyramiden sind:
- Kenntnisse über die Symmetrieigenschaften von Vielecken
- Kenntnisse über die Winkelsummen in Vielecken
- Kenntnisse über die Flächenberechnung von Vielecken
- Streckenberechnungen mithilfe des Satzes von Pythagoras
- Strecken- und Winkelberechnungen mithilfe der Winkelfunktionen sin, cos und tan
- Kenntnis der Formeln zur Berechnung des Volumens und der Oberfläche von Pyramiden.
2.1 Berechnung der Mantelfläche M und der Oberfläche O
Die Mantelfläche M einer n-seitigen regelmäßigen geraden Pyramide besteht aus n kongruenten und gleichschenkligen Dreiecken mit der Grundseite a und der Höhe hs .
Beispiel: Die Mantelfläche M einer quadratischen Pyramide mit der Grundkante a
Bei jeder Pyramide besteht die Oberfläche aus der Mantelfläche und der Grundfläche.
O = G + M
O = G + n · 1/2· a· hs
Weitere Beispiele für Oberflächenberechnungen von Pyramiden findest du hier.
2.2 Berechnung des Volumens
Für die Herleitung der Volumenformeln von Pyramiden, muss auf infinitesimale Prozesse zurückgegriffen werden.
Dies wird im Kerncurriculum für den mittleren Bildungsabschluss in Baden Württemberg nicht vorausgesetzt.
In der Unterrichtspraxis wird meist auf Plausibilitätsbetrachtungen zurückgegriffen.
Eine Möglichkeit für eine Herleitung in der Realschule bietet der Sonderfall, bei dem ein Würfel durch die Raumdiagonalen in sechs volumengleiche Pyramiden aufgeteilt wird.
Eine Präsentation dazu findet man hier ![]()
Vergleicht das Volumen einer Pyramide mit dem Volumen eines Prismas mit gleicher Grundfläche und Höhe so gilt:
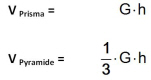
Links zu Herleitungen der Volumenformel von Pyramiden:
Heinz Schumann: Anwendungen des Prinzips von Cavalieri in computergrafischer Darstellung
mathsrv.ku-eichstaett.de
2.3 Pyramidenlinks
Links auf weitere Seiten zu diesem Thema finden Sie hier.
2.4 Berechnungen an Pyramiden
Arbeitsblatt mit Lösungen: Berechnungen an Pyramiden ![]()
Modelle: Mantelflächen zum Ausschneiden ![]()



