Der Höhensatz des Euklid

Der Höhensatz des Euklid ist der neben dem Satz des Pythagoras und dem Kathetensatz des Euklid der dritte geometrische Lehrsatz aus der Satzgruppe des Pythagoras. Mit dem Satz des Pythagoras lässt er sich recht einfach beweisen (siehe unten).

Animation: Höhensatz-Figur

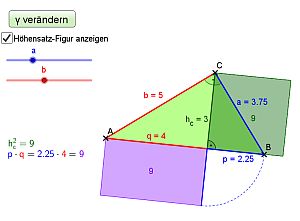
Wichtige Begriffe zum Höhensatz des Euklid:

In einem rechtwinkligen Dreieck mit den Katheten a und b sowie der Hypotenuse c teilt die Höhe h_c (über der Seite c) die Hypotenuse in zwei Hypotenusenabschnitte p ("unterhalb der Kathete a") und q ("unterhalb von b").

Die Aussage des Höhensatzes des Euklid (mit den obigen Bezeichnungen):

Beim einem rechtwinkligen Dreieck entspricht die Fläche des Höhenquadrates über der Seite c genau der Fläche des Rechtecks mit der Länge und Breite der beiden Hypthenusenabschnitte.

Mit den üblichen Beschriftungen gilt: h²=p*q

Beweis:

Die Höhe h_c teilt das Dreieck ABC in zwei rechteckige Dreiecke. (Die Katheten des großen Dreiecks werden hierbei zu Hypothenusen).
Setzt man die Pythagoras-Gleichungen der kleinen Dreiecke in die Pythagoras-Gleichung des großen Dreiecks ein und drückt die Hypotenuse c durch die beiden Hypotenusenabschnitte aus, folgt die Aussage des Höhensatzes nach Anwendung der ersten binomischen Formel.

Übungsaufgaben:

1. Beweise den Höhensatz mit Hilfe der Aussage des Satzes von Pythagoras.
   Tipp: Teile die Hypotenuse mit Hilfe der Höhe h_c in zwei Hypotenusenabschnitte und verwende, dass das Dreieck ABC hierdurch in zwei rechtwinklige Dreiecke mit einer gemeinsamen Kathete aufgeteilt wird. Durch Addition mehrere Gleichungen erfolgt der Beweis mit Hilfe einer binomischen Formel.
2. Beweise den Höhensatz mit Hilfe von ähnlichen Dreiecken.
   Tipp: Gehe vor wie bei Aufgabe 1 und verwende, dass alle drei Dreiecke zueinander ähnlich sind(warum?). Bei ähnlichen Figuren gilt die Streckenverhältnistreue.
   Erstelle den Beweis möglichst selbstständig. Zur Unterstützung bieten wir eine animierte Anleitung des Ähnlichkeitsbeweises zum Höhensatz.
3. Konstruiere zu einem Rechteck mit den Seiten p=3 und q=4 das flächengleiche Quadrat.
   Tipp: Verwende für die Dreieckskonstruktion einen Thaleskreis.
4. Wie kann man zu jeder beliebigen positiven Zahl die zugehörige Quadratwurzel mit Hilfe des Höhensatzes des Euklid konstruieren?
5. Konstruiere auf zwei verschiedene Arten zu einem gleichschenkligen Trapez und einen regelmäßigen Rechteck ein flächengleiches Quadrat. Verwende hierbei einmal den Höhensatz und einmal den Kathetensatz des Euklid.