Zur Satzgruppe des Pythagoras zählen neben dem Satz des Pythagoras zwei weitere geometrische Sätze: der Kathetensatz des Euklid und der Höhensatz des Euklid. Alle drei Sätze sind eng verwandt und können relativ einfach voneinander abgeleitet werden.

Der Satz des Pythagoras

Sicherlich gehört der Satz des Pythagoras zu den wichtigsten mathematischen Sätzen überhaupt. Er wurde auf mehrere hundert (!) verschiedene Arten bewiesen. Seine einfache Aussage lässt sich mit Hilfe der so genannten "Pythagoras-Figur" anschaulich darstellen.

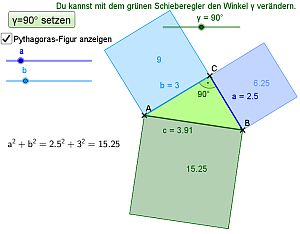
Animation: Pythagoras-Figur / Veranschaulichung der Pythagoras-Gleichung

Die Aussage des Satzes des Pythagoras:

In einem rechtwinkligen Dreieck mit den Kathetenlängen a und b
und der Hypotenusenlänge c gilt:  a²+b²=c².

in anderen Worten:

Beim einem rechtwinkligen Dreieck ergibt die Summe der
Flächeninhalte der Quadrate über den Katheten stets
den Flächeninhalt des Quadrates über der Hypotenuse.

Unter dem nebenstehenden Link findest du eine Vielzahl von animierten Beweisen zum Satz des Pythagoras.

Animierte Beweisvarianten zum Satz des Pythagoras

Achtung: der Satz des Pythagoras sagt nicht aus, dass jedes Dreieck, bei dem die Pythagoras-Gleichung gilt, auch rechtwinklig sein muss! Diese Folgerung erfordert die

Umkehrung des Satzes des Pythagoras:

Gegeben ist ein Dreieck mit den Seitenlängen a, b und c.
Wenn a²+b²=c² gilt, dann ist das Dreieck rechtwinklig mit der Hypotenuse c.

Beweis des Kehrsatzes:
Wir gehen zunächst davon aus, dass es ein Dreieck mit den Seiten a, b und c gibt, bei dem die Pythagoras-Gleichung gilt. Wir werden zeigen, dass dieses rechtwinklig sein muss.
Sicherlich gibt es ein rechtwinkliges Dreieck mit gleich langen Seiten a und b. Bei diesem rechtwinkligen Dreieck gilt (nach dem Satz des Pythagoras) die Pythagoras-Gleichung. Das heißt aber, dass auch die dritte Seite gleich lang ist, wie die Seite c des Ausgangsdreiecks. Somit sind alle drei Seiten der beiden Dreiecke gleich lang.
Der Kongruenzsatz sss begründet, dass auch die jeweiligen Winkel der Dreiecke gleich groß sein müssen. Damit ist unser Dreieck als rechtwinkliges Dreieck "überführt".

q. e. d. - quod erat demonstrandum (lat. für "was zu zeigen war")

Übungsaufgaben:

1. Joachim Fröhlich bietet auf seiner Homepage ein pdf-Dokument mit einer Vielzahl unterschiedlicher Aufgaben zur Satzgruppe des Pythagoras an. Dazu existiert ein Visual-Basic-Programm, mit dessen Hilfe die Lösungen am PC kontrolliert werden können. Link zum 22-seitigen PDF-Dokument von J. Fröhlich
2. Beweise den Satz des Pythagoras auf drei verschiedene Arten. Verwende als Hilfe die animierten Beweisvarianten .
3. Drei positive natürliche Zahlen a, b und c, die die Pythagoras-Gleichung erfüllen, bilden ein so genanntes pythagoräisches Zahlentripel. Zeige, dass man für beliebige, positive natürliche Zahlen p und q (mit p>q) solch ein Zahlentripel mit den Formeln a=p²-q²; b=2*p*q und c=p²+q² findet.
4. Oben siehst du einen Beweis der Umkehrung des Satzes des Pythagoras . Begründe die Aussage dieser Umkehrung auf eine andere Art mit Hilfe der Animation zur Veranschaulichung der Pythagoras-Figur.
5. Suche nach Anwendungsaufgaben oder Fragestellungen, bei denen der Satz des Pythagoras zur Problemlösung führt. (Verwende hierzu dein Buch).