Der Kathetensatz des Euklid

Der Kathetensatz des Euklid zählt zur Satzgruppe des Pythagoras, da man mit ihm den Satz des Pythagoras beweisen kann. Umgekehrt gehen die Gleichungen des Kathetensatzes direkt aus der Aussage des Satzes des Pythagoras hervor (siehe Übungsaufgabe unten).

Würde der Kathetensatz nicht gelten, könnte auch der Satz des Pythagoras nicht richtig sein. Die beiden Sätze (und auch der Höhensatz des Euklid) können somit direkt ineinander überführt werden.

Animation: Kathetensatz-Figur

Wichtige Begriffe zum Kathetensatz des Euklid:

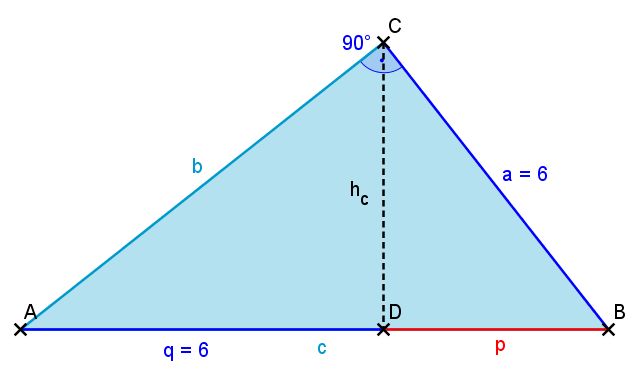
In einem rechtwinkligen Dreieck mit den Katheten a und b sowie der Hypotenuse c teilt die Höhe h_c (über der Seite c) die Hypotenuse in zwei Hypotenusenabschnitte p ("unterhalb der Kathete a") und q ("unterhalb von b").

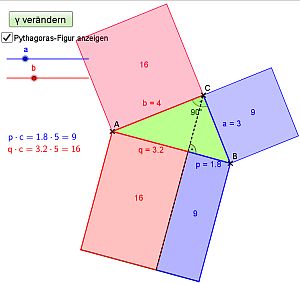
Die Aussage des Kathetensatzes des Euklid:

Beim einem rechtwinkligen Dreieck mit den Katheten a und b
und der Hypotenuse c teilt die Verlängerung der Höhe h_c
das Hypotenusenquadrat in zwei Rechtecke.
Die Fläche eines Kathetenquadrates stimmt mit der entsprechenden
Rechtecksfläche unter dem zugehörigen Hypthenusenabschnitt überein.

Mit den üblichen Beschriftungen gilt: a²=p*c bzw. b²=q*c

Beweis:

Eine animierte Variante des historischen Beweises von Euklid (mit Scherung und Drehung) findest du hier:

Beweis Satzes von Pythagoras und des Kathetensatzes nach Euklid.

Übungsaufgaben

1. Beweise den Kathetensatz mit Hilfe von ähnlichen Dreiecken.
   Tipp: Teile die Hypotenuse mit Hilfe der Höhe h_c in zwei Hypotenusenabschnitte und verwende, dass das Dreieck ABC hierdurch in zwei rechtwinklige Dreiecke aufgeteilt wird. Die beiden kleinen Dreiecke sind dabei ähnlich zum Dreieck ABC.
   Erstelle den Beweis wenn möglich selbstständig. Zur Unterstützung bieten wir eine animierte Anleitung des Ähnlichkeitsbeweises zum Kathetensatz.
2. Konstruiere mit Hilfe des Kathetensatzes ein Quadrat der Fläche 15 Flächeneinheiten.
3. Begründe mit dem Kathetensatz: "Genau dann, wenn die Höhe eines rechtwinkligen Dreiecks die Hypothenuse im Verhältnis des Goldenen Schnitts teilt, ist eine Kathete gleich lang, wie ein Hypothenusenabschnitt (siehe nachfolgende Skizze).