Hauptseite Trigonometrie
Die Trigonometrie (in der Schule) beschäftigt sich mit der Bestimmung von Längen und Winkeln. Unsere Schüler kennen bereits die Kongruenzabbildungen (Drehung, Verschiebung sowie Punkt- und Achsenspiegelung). Diese Abbildungen sind "winkeltreu" und "längentreu".
Verzichtet man auf die "Längentreue", kommt man zu den Ähnlichkeitsabbildungen. Diese lassen die Winkelgrößen unverändert. Die "Längentreue" kann durch die "Längenverhältnistreue" ersetzt werden.
Trigonometrie am rechtwinkligen Dreieck
Die Längenverhältnistreue ist (zunächst) die Grundlage der Definitionen für unsere elementaren Winkelfunktionen am rechtwinkligen Dreieck (Sinus, Kosinus und Tangens)
Seitenbeziehungen am rechtwinkligen Dreieck (mit Animation und Übungsaufgaben).
Übungen für die Realschule
Definitionserweiterung für beliebige Winkel - mit Lernvideos
Bei der Definitionserweiterung kommt auf den Einheitskreis eine besondere Rolle zu. Die Koordinaten eines Punktes auf diesem Kreis liefern ab sofort die neue Definition für unsere "neuen" Funktionen
Definitionserweiterung bei trigonometrischen Funktionen - mit Lernvideo.
Lernumgebung: Trigonometrische Funktionen im Bogenmaß
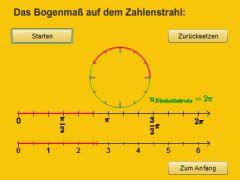
Im Bogenmaß lassen sich Winkel ebenso beschreiben wie mit Winkeln im Gradmaß. Diese Vorgehensweise liefert vor allem in der Sekundarstufe 2 beim Differenzieren und Integrieren viele Vorteile. Unter folgendem Link finden Sie unter anderem eine vertonte Flash-Animation, mit der die wichtigen pi/6-Abschnitte motiviert und sowohl am Kreis, als auch auf dem Zahlenstrahl dargestellt werden.
Lernumgebung: Winkelangaben im Bogenmaß
Die Schaubilder der Sinus- Kosinus- und Tangensfunktion
Wie hängen die Schaubilder unserer trigonometrischen Funktionen mit den Definitionen zusammen. Betrachte für den Zusammenhang Schaubild-Einheitskreis die dynamischen GeoGebra-Grafiken
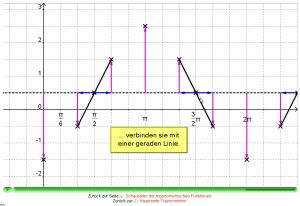
Lernvideo: Sinus- und Kosinuskurve von Hand zeichnen

Zum Youtube-Lernvideo: "Sinus- und Kosinuskurve von Hand zeichnen"
Verschiebung und Streckung der Sinusfunktion (mit Lernvideo)
Durch Verschiebung und Streckung des Schaubildes der Sinusfunktion lassen sich viele periodische Vorgänge in unserer Alltagswelt beschreiben. Dies führt zur Gleichung der allgemeinen Sinusfunktion. Anhand eines Beispieles wird die Vorgehensweise bei der Ermittlung der Funktionsgleichung zu einem vorgegebenen Schaubild aufgezeigt. Verschiebung und Streckung des Schaubildes der Sinusfunktion.
Beachten Sie in diesem Zusammenhang auch das zugehörige Lernvideo