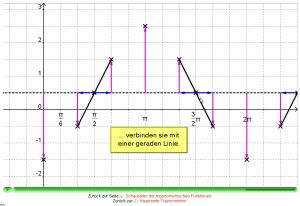
Schaubilder der trigonometrischen Funktionen
Wie bei allen mathematischen Funktionen lässt sich der Verlauf der trigonometrischen Funktionen mit Hilfe eines Schaubildes veranschaulichen. Die Sinus- und Kosinuskurve sowie das Schaubild der Tangensfunktion gehören zum Grundwissen eines jeden Abiturienten.
Trigonometrische Schaubilder und der Einheitskreis
Normalerweise benötigt man für die Erstellung eines Schaubildes eine Wertetabelle. Bei den trigonometrischen Funktionen sollte man sich bei der Schaubilderstellung den Funktionsverlauf auch mit Hilfe des Einheitskreises verdeutlichen. Dieser Zusammenhang ist elementar und wird immer wieder bei Anwendungsaufgaben (nicht nur in der Physik) benötigt.
Zur Vorbereitung auf die Animation ist die Wiederholung des Zusammenhanges zwischen Winkel- und Bogenmaß sinnvoll. Hierzu finden eine vertonte Animation: Winkelangaben im Bogenmaß.
Einteilung der Koordinatenachsen
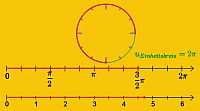
Meist muss das Schaubild einer Sinus- oder Kosinusfunktion über eine Periode gezeichnet werden. Diese Länge von 2pi stimmt nicht mit unseren Kästcheneinteilungen im karierten Heft überein. Wir sollten daher 2pi auf 6 runden. In diesem Fall benötigt man für eine vollständige Periode etwas mehr als 12 Kästchen, also 6 cm Platz. Dann entspricht eine Kästchenbreite dem Wert pi/6. (Siehe vertonte Animation zu wichtigen Winkelwerten im Bogenmaß).
Denkbar ist auch eine "vergrößerte Darstellung" durch eine Unterteilung der Periode in 12 pi/6-Schritte. Bei der Hochachseneinteilung sollte dann eine Längeneinheit 2cm lang sein. Die für die x-Achse werden in diesem Fall mindestens 12cm benötigt, für die y-Achse sind es mindestens 4cm.
Die "Ein Drittel - ein Halb - Regel" bei Sinus und Kosinus
Gelegentlich muss man auch in den Zeiten des grafikfähigen Taschenrechners ein Schaubild zeichnen. Beim Schaubild der Sinus- und Kosinusfunktion ist die "1/3 - 1/2 Regel" eine große Hilfe:
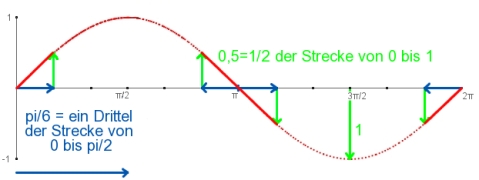
Gehe von einer Nullstelle auf der x-Achse 1/3 des Weges in Richtung der Stelle mit den nächsten Extrempunkt, dann ist hier bereits die Hälfte des y-Wertes dieses Extrempunktes erreicht. Die Steigung der Kurve ist in diesem Bereich nahezu konstant.
Somit muss man beim Zeichnen der Schaubilder neben diesen "Geradenstücken" nur noch die "runden Kappen" um die Extrempunkte zeichnen.
Lernvideo: Das Schaubild der Sinusfunktion im Bogenmaß zeichnen - zum Teil mit Lineal
Beim Zeichnen der Schaubilder von Sinus und Kosinus hilft dir die obige 1/3-1/2-Regel. Teile dafür die x-Achse geschickt ein, so dass eine Periode die Länge von 12 Kästchen besitzt.
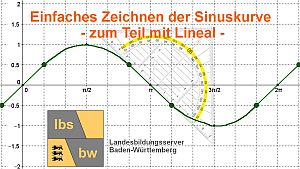
Zum Lernvideo: "Das Schaubild der Sinusfunktion im Bogenmaß von Hand zeichnen"
Lernvideo: Schaubild einer gestreckten und verschobenen Sinusfunktion zeichnen
Eine Beschreibung der Vorgehensweise an einer Beispielfunktion finden Sie hier: