Der Umfangswinkelsatz
Aussage des Umfangswinkelsatzes:
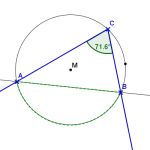
Alle Umfangswinkel (=Rand- oder Peripheriewinkel) über einem Kreisbogen sind gleich groß.
Da durch eine Kreissehne zwei Kreisbögen bestimmt werden, lautet die entsprechende Aussage: Alle Umfangswinkel auf der gleichen Seite einer Sehne sind gleich groß.
Diese Aussage lässt sich mit einer kleinen Animation sehr schön demonstrieren oder aber auch von den Schülerinnen und Schülern am PC selbst entdecken.
An der Animation ist sehr schön zu sehen, wie aus dem Umfangswinkel in den beiden Grenzfällen, wenn der Umfangswinkel auf ein Ende der Sehne fällt, ein Sehnen-Tangenten-Winkel wird.
Animation zur Aussage des Umfangswinkelsatzes
Ein sehr schöner und anschaulicher Beweis des Umfangswinkelsatzes (oft auch Randwinkel- oder Peripheriewinkelsatz)
Die folgenden Schritte begründen die Aussage des Umfangswinkelsatzes. Sie verfolgen in anschaulicher Weise einen Weg, den Winfried Haag in seinem Buch "Wege zu geometrischen Sätzen" (Klett-Verlag 2003, ISBN 3-12-720120-6) vorschlägt.
Zum Beweis:
Für den hier vorgestellten Beweis des Umfangswinkelsatzes wird lediglich Grundwissen über Punkt- und Achsenspiegelungen vorausgesetzt. Die die Gleichheit von Stufen- und Wechselwinkeln folgt aus der Winkeltreue bei Verschiebungen und Spiegelungen. Die Kenntnisse über gleichschenklige Dreiecke und das Lösen von Gleichung, die beim "üblichen" Beweis unumgänglich sind, spielen hier keine Rolle.
Ausgehend von zwei parallelen Sekanten am Kreis und zwei sich schneiden Geraden wird durch "Umlegen" von Kreisbögen die Aussage des Umfangswinkelsatzes begründet. Hierbei ergeben sich automatisch zwei interessante geometrische Tatsachen:
- der Zusammenhang zwischen Umfangswinkel und Mittelpunktswinkel über einem Kreisbogen sowie
- Erkenntnisse über Winkeleigenschaften von Sehnenvierecken.
Anwendung: Konstruktion von regelmäßigen n-Ecken mit Hilfe von Geradenbüscheln
Verschiebt man ein Geradenbüschel in der Ebene und führt anschließend eine Drehung durch, so liegen die Schnittpunkte sich entsprechender Geraden auf einem Kreis durch die Büschelzentren. Bei regelmäßigen Geradenbüscheln lassen sich auf diese Weise regelmäßige n-Ecke konstruieren. Mit Hilfe einer GeoGebra-Animation wird das Verfahren am Beispiel eines Büschels mit drei Geraden vorgestellt.
Ein Übungsblatt zum Umfangswinkelsatz mit Tipps und Hinweisen
Die Übungen dieses Arbeitsblattes verlangen die Anwendung des Umfangswinkelsatzes. Durch Beachten der Tipps können die Schüler schnell zu einer Lösung kommen.
Dokument als OpenOffice-Datei Download
Dokument als PDF Download
Anwendung des Umfangswinkelsatzes beim Beweisen
- Bei einem spitzwinkligen Dreieck ist der Höhenschnittpunkt gleichzeitig auch der Mittelpunkt des Inkreises vom Höhenfußpunktdreieck.
Für den Beweis dieser Aussage wird neben dem Umfangswinkelsatz auch der Satz über die Winkelsumme im Dreieck sowie der Thalessatz benötigt.
- Wie lässt sich mit Hilfe von Sehnenvierecken und dem Umfangswinkelsatz nachweisen, dass eine Gerade eine Dreiecksseite senkrecht schneidet? Diese mittelschwere Übung zur Beweisführung mit dem Umfangswinkelsatz und den Winkeleigenschaften von Sehnenvierecken eignet sich in besonderer Weise zur Motivation und Vorbereitung auf Wettbewerbsaufgaben.
- Der Satz des Ptolemäus ist ein bei uns recht unbekannter, aber sehr mächtiger mathematischer Lehrsatz. Er lässt sich mit Hilfe des Umfangswinkelsatzes und der Streckenverhältnistreue bei ähnlichen Figuren beweisen. Mit seinen Anwendungen erhält man "nebenbei" z. B. den golden Schnitt, die Aussagen des Kosinussatzes sowie den allseits bekannten Satz des Pythagoras.
- Animation und Lernvideo: Mit Hilfe des Umkreises und einem "Berührkreis" an eine Dreiecksseite wird ein Winkel halbiert. Dies soll in einem Beweis begründet werden. Im Beweis werden Umfangswinkel, Sehnen-Tangenten-Winkel, gleichschenklige Dreiecke und Stufenwinkel an Parallelen verwendet. Mit Hilfe einer Animation und eines Lernvideos werden die einzelnen Beweisschritte dargestellt und erläutert. Weitere Aufgaben und Fragestellungen ergänzen das Angebot. Das Lernvideo geht neben dem Beweis näher auf den Zusammenhang zwischen Umfangswinkel und Sehnen-Tangenten-Winkel ein und stellt verschiedene Werkzeuge zum Nachweis gleicher Winkel vor.
- Mit Hilfe von Ähnlichkeit und der Kenntnis des Zusammenhanges zwischen Umfangswinkel und Mittelpunktswinkel kannst du zeigen, dass das Produkt aus den drei Dreiecksseiten gleich dem Vierfachen des Produktes aus der Dreieckesfläche A und dem Umkreisradius R ist.




