Winkel
Winkel zuordnen, Winkel zeichnen und Winkel schätzen
Animierte Anleitung: Messen und Zeichnen von Winkeln mit dem Geodreieck
Wer Hilfe beim Zeichnen und Messen von Winkeln mit dem Geodreieck benötigt, findet auf GeoGebra sehr schöne Online-Materialien. Sie eignen sich hervorragend zur Präsentation im Unterricht - aber auch zum eigenständigen Lernen oder zur Wiederholung.
Wie zeichne / messe ich einen Winkel mit dem Geodreieck? via GeoGebra
Online-Übung: Innenwinkel im Dreieck mit dem Geodreieck messen
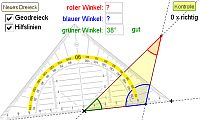
Bei der Winkelmessung mit dem Geodreieck ist die richtige Wahl der Winkelskala für viele Schüler immer wieder ein Problem. Mit der hier vorgestellten Geogebra-Online-Übung können die Messwerte sofort kontrolliert und gegebenenfalls verbessert werden. Erfolgreiche Lösungen werden mit Punkten belohnt.
Innenwinkel im Dreieck mit dem Geodreieck messen via GeoGebra
Online-Übung: Winkelgrößen schätzen - spielerisch die Vorstellungskraft verbessern
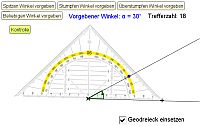
Mit Hilfe der vorgestellten Geogebra-Online-Übung kann spielerisch und schnell eine genaue Vorstellung von Winkelgrößen geschaffen werden. Das Geodreieck kann zu Beginn als Hilfswerkzeug eingesetzt werden, wird nach kurzer Zeit aber gar nicht mehr benötigt. Wer schafft die meisten "Treffer" beim "Winkel schätzen"?
Winkel schätzen (und messen) via GeoGebra
Konstruktion einer Bahnhofsuhr mit schönen Erkenntnissen für besondere Dreiecke

In einer Standardaufgabe zur Anwendung von Winkelkonstruktionen werden die Schüler aufgefordert, das Ziffernblatt einer Bahnhofsuhr zu zeichnen. Lässt man hier der Phantasie der Schülerinnen und Schüler freien Lauf, entwickeln sie wunderbare Lösungsvorschläge.
Bei folgendem Lösungsweg werden zwei Erkenntnisse auf dem Silbertablett präsentiert - sie sollten unbedingt "mitgenommen" werden:
Konstruiert man auf kariertem Papier einen Kreis um einen Gitterpunkt mit einem ganzzahligen Radius (zwei Kästchen sollten eine Längeneinheit beschreiben), kann das Ziffernblatt ohne Winkelmessung konstruiert werden, denn betrachtet man den Radius als Hypotenuse eines 30°-Dreiecks, dann trifft diese bei einer horizontalen (oder vertikalen) Ankathete auf die "Karolinien". Hierbei sollte man festhalten:
- Bei einem rechtwinkligen 30°-Dreieck ist die kurze Seite stets halb so lang wie die lange.
- Spielgelt man ein rechtwinkliges 30°-Dreieck an der mittleren Seite, so erhält man ein gleichseitiges Dreieck.
Nachfolgend bieten wir Ihnen ein Arbeitsblatt mit der entsprechenden Aufgabenstellung sowie eine Zusammenfassung der möglichen Nachbetrachtungen mit Ergebnissicherung zum Download an.
Arbeitsblatt als OpenOffice-Datei Download 100 KB
Arbeitsblatt als PDF-Datei Download 52 KB
Arbeitsblatt mit Lösungsvorschlag als OpenOffice-Datei Download 112 KB
Arbeitsblatt mit Lösungsvorschlag als PDF-Datei Download 67 KB
Preisgekrönter E-Learning-Kurs "Willi Winkel"
Der interaktive Kurs "Mathematik mit Willi Winkel" wurde von vier Wiener Lehrkräften - Julia Schrittwieser, Michaela Kaiser, Irene Tatzgern und Christian Nosko - mit Unterstützung des MNI-Fonds für die Einführung des Winkelbegriffs (in Klasse 6) entwickelt.
Die Texte sind verständlich verfasst und die Seiten sind ansprechend, anschaulich und vor allem auch interaktiv gestaltet. Die Inhalte sind in "Tagespackungen" gegliedert. Arbeitsblätter sichern jeweils den Lernerfolg.
Der E-Learning-Kurs möchte zu einer selbstständigen und aktiven Aneignung von Kenntnissen und Fertigkeiten anregen.
E-Learning-Kurs Willi Winkel via Milli´s LernBAR
Herausgeber: Landesbildungsserver Baden-Württemberg
Quelle: https://www.schule-bw.de
Bitte beachten Sie eventuell abweichende Lizenzangaben bei den eingebundenen Bildern und anderen Dateien.





