Tangentenkonstruktionen am Kreis mit Zirkel und Lineal
Bei der Konstruktion der Kreistangente müssen zwei Fälle unterschieden werden:
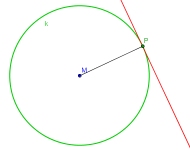
Fall 1: Gesucht ist die Tangente durch einen Punkt P, der auf der Kreislinie liegt (d. h. der Berührpunkt ist bekannt).
Tangentenkonstruktion bei bekanntem Berührpunkt
Fall 2: Gesucht ist eine Tangente durch einen Punkt P, der nicht auf der Kreislinie liegt (Berührpunkt unbekannt).
Bei Fall 2 gibt es wiederum zwei Unterfälle. Einer davon ist trivial:
Liegt der Punkt P innerhalb des Kreises gibt es keine Tangente, denn in diesem Fall schneidet jede Gerade durch P den Kreis in genau zwei Punkten. Damit sind alle Geraden durch P Sekanten (Geraden mit genau zwei Kreisschnittpunkten).
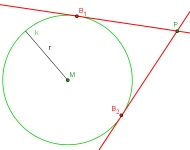
Im zweiten Fall ist eine Tangente durch einen Punkt außerhalb des Kreises gesucht. Der Berührpunkt der Tangente mit dem Kreis ist nicht bekannt. In diesem Fall gibt es unter allen Geraden durch P Sekanten, Passanten (=Geraden ohne Berühr- oder Schnittpunkt mit dem Kreis) sowie genau zwei Tangenten. Diese gilt es zu konstruieren.



