Dreieckszahlen

Was sind Dreieckszahlen?

Addiert man die ersten 5 natürlichen Zahlen (also 1+2+3+4+5), so erhält man die Zahl 15. Das ist die 5. Dreieckszahl - weshalb? Dies wird klar, wenn man jede Zahl als eine Gruppe von Punkten interpretiert und diese Punkte in einer geeigneten Weise anordnet.

Betrachte hierzu die nachfolgende Animation.

Animation zu den Dreickszahlen

Die Gaußsche Summenformel für Dreieckszahlen
("der kleine Gauß")

Zur Berechnung einer beliebigen (n-ten) Dreieckszahl D(n) kann man die Gaußsche Summenformel verwenden (siehe Grafik rechts).
Man erzählt sich die Geschichte, dass der damals neunjährige Carl Friedrich Gauß diese Formel gefunden hat, als er im Mathematikunterricht die Summe der ersten 100 natürlichen Zahlen berechnen sollte. Felix Breuer erzählt in seinem Lernvideo die nette Geschichte sehr schön und erklärt leicht verständlich die Gültigkeit der Formel.

Beweis der Formel:

Wir verdoppeln das Dreieck, so dass ein Rechteck mit 2*D(n) Punkten entsteht. Die Höhe des Rechtecks ist n, die Breite (n+1). Somit enthält das Rechteck n*(n+1) Punkte.

Die n-te Dreieckszahl ist die Hälfte dieser "Rechteckszahl", also 1/2*n*(n+1).

Hinweis:

Beim Produkt einer Zahl mit ihrem Nachfolger ist immer einer der Faktoren gerade. Bei der Berechnung der Hälfte dieses Produktes sollte man zuerst die gerade Zahl halbieren und dann mit der ungeraden Zahl multiplizieren.

Beispiel:

n=15: -> 15. Dreieckszahl = D(15) = 1/2*15*16=15*8=120.

Schöne Anwendungen zu den Dreieckszahlen

Auf einer Party sind 15 Gäste. Sie möchten mit Ihren Gläsern anstoßen. Wie oft erklingt das Glas?

Diese kombinatorische Fragestellung wird in der Mathematik als "Sektglasproblem" bezeichnet. Das Anstoßen mit Sekt könnte man durch Begrüßungen per Handschlag ersetzten. Auf diese Art erhält man das mathematische "Handschlagproblem".

Die Frage nach den Anzahlen ist für den Laien zunächst kaum lösbar. Reduziert man das Problem jedoch auf weniger Personen, erkennt man schnell Gemeinsamkeiten mit den Dreieckszahlen.

Aber Achtung: es gibt einen Unterschied: Eine Person kann nicht mit sich selbst anstoßen (bzw. sich nicht selbst per Handschlag begrüßen).

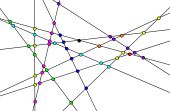
Bei den Dreieckszahlen haben wir jede natürliche Zahl durch eine Anzahl an Punkten dargestellt. Nun können wir jede Person durch eine Gerade darstellen. Auf diese Weise führt die Fragestellung nach der maximalen Anzahl an Schnittpunkten zur Lösung unserer oben beschriebenen Probleme.

Animation max. Zahl an Schnittpunkten bei n Geraden

Anspruchsvolle Übungsaufgabe zu den Rechengesetzen

Thomas rechnet die Zahlen von 1 bis 30 mit einem Rechentrick zusammen. Er bildet Pärchen und zwar addiert er die erste mit der letzten, die zweite mit der vorletzten, die dritte mit der drittletzten Zahl usw. Anschließend multipliziert er das Ergebnis eines dieser Paare mit 15.
Auf welche Zahl kommt Thomas?
Führe die Rechnungen von Thomas im Heft schrittweise durch.
Wo wendet er welche Rechengesetze an?

Mit Hilfe dieser schönen Aufgabe kann man den Schülern schon in den unteren Klassen zeigen, an welchen Stellen beim Rechnen die Rechengesetze angewendet werden.

als OpenOffice-Datei Download
Dokument als PDF Download

2016 ist eine Dreieckszahl!

2016 ist das Jahr einer Dreieckszahl. Diese Behauptung lässt sich begründen, indem man schrittweise die Folge der Dreieckszahlen berechnet und dabei schließlich auf 2016 stößt.
Ab der achten Klasse bist du in der Lage, quadratische Gleichungen zu lösen. Verwende zunächst die Formel D(n)=0,5*n*(n+1) zur direkten Bestimmung von Dreieckszahlen. Diese führt durch Ausmultiplizieren auf eine quadratische Gleichung, die sich mit der p-q-Formel oder der abc-Formel lösen lässt.

Zusatzfrage:

Wie viele Partygäste müssen miteinander anstoßen, damit die Gläser genau 2016-mal erklingen? (Je zwei Gäste sollen dabei genau ein mal miteinander anstoßen).

Lösungsvorschlag:

Dokument als OpenOffice-Datei Download
Dokument als PDF Download

Das Pascalsche Dreieck

Das Pascalsche Dreieck sieht zunächst wie eine einfache Zahlenspielerei aus. Im Laufe der gymnasialen Schullaufbahn erkennen viele Schüler, dass es sehr viele überraschende und faszinierende Eigenschaften besitzt. Eine dieser Eigenschaften ist das Vorhandensein der Dreieckszahlen.
Unter dem nachfolgenden Link findest Du ein großes Pascalsches Dreieck sowie viele weitere Besonderheiten und Informationen.

Zum Pascalschen Dreieck