Die quadratische Gleichung des Goldenen Schnitts

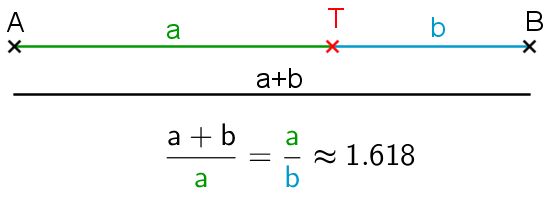
Bei der Suche nach einer exakten Zahl für den Goldenen Schnitt musst du das Verhältnis a/b durch eine Variable ersetzen:

Diese Substitution vereinfacht die Verhältnisgleichung (a+b)/a=a/b und führt zu einer Bruchgleichung (mit der Variablen im Nenner):

Multipliziere im nächsten Schritt beide Seiten mit x. (Das ist erlaubt, da x für den Goldenen Schnitt steht und nicht null sein kann).

Diese quadratische Gleichung musst du für die p-q-Formel vorbereiten, so dass auf der rechten Seite null steht. Subtrahiere daher auf beiden Seiten der Gleichung x und 1.

Diese Gleichung bezeichnen die Mathematiker als quadratische Gleichung des Goldenen Schnitts.
Mit der p-q-Lösungsformel erhältst du zwei Lösungen:

Wurzel 5 ist etwas größer als 2. Damit ist Lösung mit dem Minuszeichen negativ und als Verhältnis zweiter (positiver) Strecken nicht geeignet.

Die Lösung mit dem Pluszeichen hingegen ist die exakte Zahl für den Goldenen Schnitt.

Da Wurzel 5 eine irrationale Zahl ist, ist auch der Goldene Schnitt eine irrationale Zahl.