Der goldene Schnitt
Als "Goldenen Schnitt" bezeichnen wir ein ganz besonderes Teilungsverhältnis, bei dem sich das Ganze zum größeren Teil genau so verhält, wie der größere Teil zum kleineren.
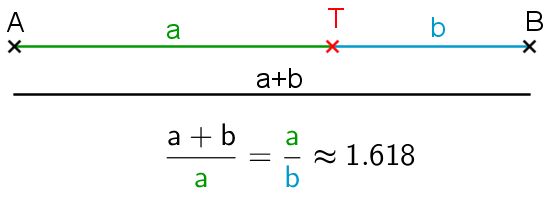
Eine animierte Anleitung zur Konstruktion dieser Teilung im Goldenen Schnitt findest du weiter unten oder über den Link im Navigationsbereich der rechten Randspalte.
Den Näherungswert des Goldenen Schnitts von 1,618 kannst du dir als Anteil vorstellen: Das Ganze ist ungefähr das 1,618-fache des größeren Teils und somit um ca. 61,8% größer. Ebenso ist der größere Teil um 61,8% größer als der kleinere Teil.
(Zum Vergleich: bei einem 16:9 Bildschirm beträgt die Bildschirmbreite das 16/9-fache der Bildschirmhöhe (16/9=1,777...) und ist daher um ca. 77,8% größer).
Die quadratische Gleichung des Goldenen Schnitts
![]()
Das exakte Verhältnis des Goldenen Schnitts ist eine Zahl, die ebenfalls als Goldener Schnitt bezeichnet wird. Zur exakten Berechnung dieser Zahl musst du mit Hilfe der im oberen Abschnitt angegebenen Verhältnisgleichung eine (quadratische) Gleichung aufstellen. Diese wird anschließend mit der bekannten Lösungsformel gelöst.
Die genaue Vorgehensweise mit der zugehörigen Lösung wird auf der Seite des nachfolgenden Links beschrieben. Darüber hinaus findest du eine Begründung, warum der Goldene Schnitt eine irrationale Zahl ist.
Die quadratische Gleichung des Goldenen Schnitts
Konstruktion des Goldenen Schnitts / Teilung einer Strecke im Verhältnis des Goldenen Schnitts mit Zirkel und Lineal
Du kannst eine gegebene Strecke sehr leicht im Goldenen Schnitt teilen. Wie du dabei vorgehen musst, wird in der nachfolgend vorgestellten Animation schrittweise gezeigt.
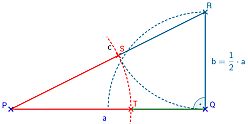
Die rechnerische Begründung ist nicht ganz einfach, aber mit dem notwendigen Grundwissen eine schöne Anwendung und Wiederholung der Lerninhalte aus den Klassenstufen 8 und 9 (Gymnasium).
Animation: Konstruktion des Goldenen Schnitts mit Zirkel und Lineal (mit rechnerischer Begründung)
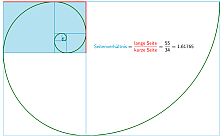
Seitenverhältnisse von Fibonacci-Rechtecken als Näherung für den Goldenen Schnitt (mit Fibonacci-Spirale)
Die Zahlenfolge 1; 1; 2; 3; 5; 8; 13; ... wird Fibonacci-Folge genannt. Mit diesen Zahlen lassen sich mit Quadraten immer größer werdende Rechtecke zeichnen, deren Verhältnisse eine Näherung für den Goldenen Schnitt liefern.
Der Goldene Schnitt im Pentagramm (Drudenfuß)
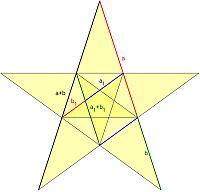
Markiert man auf einer Kreislinie in gleichen Abständen 5 Punkte, so können diese mit einem Strich zu einem regelmäßigen Stern, dem so genannten Pentagramm (auch Drudenfuß), verbunden werden.
Das Pentagramm enthält den Goldenen Schnitt in den Verhältnissen seiner Längen. Interessant sind hierbei auch geschichtliche Aspekte.
Genauere Informationen mit einer Animation liefert die folgende Seite zum Thema
Der Goldene Schnitt im Pentagramm (mit Animation)
Herausgeber: Landesbildungsserver Baden-Württemberg
Quelle: https://www.schule-bw.de
Bitte beachten Sie eventuell abweichende Lizenzangaben bei den eingebundenen Bildern und anderen Dateien.



