Grafisches Lösen von Gleichungen mit Funktionen
Vorbemerkung:
Das grafische Lösen von Gleichungen ist eine hilfreiche Alternative zu den algebraischen Methoden. Stärkt es doch die Fähigkeit, Funktionstypen mit ihren Schaubildern zu verbinden und die Lösbarkeit bzw. Nicht-Lösbarkeit von Gleichungen geometrisch zu begründen.
In Zeiten von Computer, CAS-Rechner und grafikfähigem Taschenrechner bietet das grafische Lösungsverfahren eine zeitsparende Alternative zu den algebraischen Lösungsmethoden. Darüber hinaus eignet es sich besonders für Gleichungen, bei denen keine algebraischen Lösungsformeln existieren.
Das grafische Lösungsverfahren:
Du musst beim grafischen Lösen einer Gleichung jede Seite der Gleichung als Funktion interpretieren. Gib diese Funktionen in den beiden farbigen Eingabefenstern der nachfolgenden Animation ein. Eventuelle Schnittpunkte erscheinen in roter Farbe. Eventuell musst du die Fenstereinstellungen anpassen, um alle Schnittpunkte zu finden. Die Lösungen der Gleichung (unter Umständen gerundet) kannst du aus den x-Werten der Schnittpunkte näherungsweise ablesen. Falls die Markierung bei "Lösungsmenge anzeigen" gesetzt ist, wird diese auch angezeigt.
Die Gleichung ist nicht lösbar, wenn die Schaubilder sich nicht schneiden.
Mit dem Symbol 
(oben rechts) kann die Zeichenfläche "gereinigt" werden.
Aufgaben:
- Löse die folgenden Gleichungen grafisch mit Geogebra.
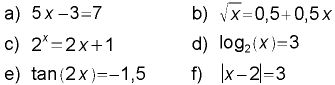
- Erfinde eigene Gleichungen und löse sie.
- Löse die erste Gleichung von Aufgabe 1 rechnerisch in mehreren Schritten und veranschauliche die einzelnen Rechenzeilen Schritt für Schritt mit Hilfe der Schaubilder. Was verändert sich, was bleibt gleich? Warum muss das so sein?
- Welche Nachteile besitzt das grafische Lösungsverfahren gegenüber dem rechnerischen?