Definitionsmenge bei Wurzelgleichungen bestimmen
Warum muss man bei Wurzelgleichungen die Definitionsmenge angeben?
Der Radikant einer Wurzel darf niemals negativ werden. In solch einem
Fall ist eine Wurzel nicht definiert und die zugehörige Gleichung nicht
definiert.
Aus diesem Grund muss man bei Wurzelgleichungen die Definitionsmenge
angeben.
Wie bestimmt man die Definitionsmenge bei Wurzelgleichungen?
Da der Radikant ("das" unter der Wurzel) stets größer oder gleich null sein muss, ist es schlau, wenn man die Definitionsmenge in einer Nebenrechnung über eine Ungleichung bestimmt.
Achtung:
- Multipliziert man eine Ungleichung mit einer negativen Zahl (dividiert man durch eine negative Zahl), so wechselt das Ungleichzeichen seine Richtung. (In den meisten Fällen kann man solch eine Multiplikation mit einer Addition vermeiden.)
- Multipliziere oder dividiere möglicht nicht mit einem Ausdruck, der eine Variable enthält. In solch einem Fall muss man verschiedene Fallunterscheidungen machen:
- der Ausdruck ist positiv - negativ (-> Richtungswechsel des Ungleich-Zeichens)
- der Ausdruck ist null (-> Umformung nicht erlaubt -> untersuche den Fall durch Einsetzten der entsprechenden Zahl. Überprüfe ob in diesem Fall die Gleichung erfüllt ist.
Wie gibt man eine Definitionsmenge an?
In den meisten Fällen besteht die Definitionsmenge aus allen reellen Zahlen, die größer gleich (bzw. kleiner gleich) einer reellen Zahl sind. Hierfür gibt es in der Mathematik eine festgelegte Mengenschreibweise.
Die Menge alle reellen Zahlen größer gleich 5 schreiben wir:
Oft besteht die Definitionsmenge aus allen positiven (negativen) reellen Zahlen sowie der Null. Dies kann man auf die folgende Art sehr kurz beschreiben. (Der Index 0 ist nicht zwingend, verdeutlicht aber, dass die Null in der Definitionsmenge enthalten ist.)
Musteraufgaben zur Bestimmung der Definitionsmenge
Aufgabe 1:
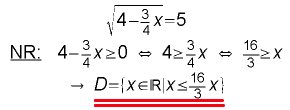
Aufgabe 2:
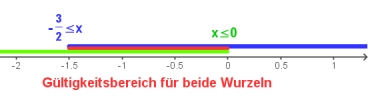
Tauchen in der Gleichung mehrere Wurzeln auf, so besteht die Definitionsmenge aus denjenigen Zahlen, für die beide Radikanten größer gleich null sind.
(Achtung, wenn bei einer Ungleichung mit einer negativen Zahl multipliziert wird - alternativ könnte man bei NR2 auch zunächst 1/2 x addieren und anschließend die Ungleichung mit 2 multiplizieren.)
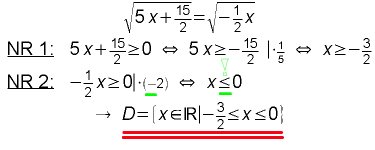
Der gemeinsame Gültigkeitsbereich für beide Wurzeln lässt sich am Zahlenstrahl veranschaulichen.