Die Kreiszahl pi
Laut Definition besitzt ein Kreis mit dem Radius von einer Längeneinheit (Einheitskreis) exakt pi Flächeneinheiten.
Zur näherungsweisen Bestimmung der Kreiszahl pi benötigt man daher ein Verfahren zur Berechnung der Kreisfläche.
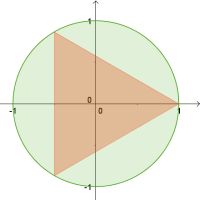
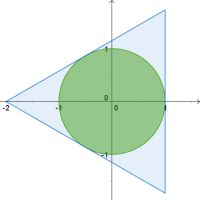
Näherung durch ein- und umbeschriebene Vielecke
Die beiden Animationen
und
beschreiben hierfür zwei Möglichkeiten.
Die nachfolgenden Aufgaben ermöglichen eine Vernetzung des Themas u. a. mit der Prozentrechnung und der Fehlerrechnung.
Weitere Verständnisfragen und Aufgaben werden von der Mathematik-Redaktion gerne angenommen und veröffentlicht Mail an Redaktion Mathematik.
Aufgaben:
- Bei jedem rechtwinkligen 30°-Dreieck ist die kürzeste Seite genau halb so lang wie die längste. Warum folgt aus dieser Tatsache unmittelbar, dass das einbeschriebenen 12-Eck die Fläche 3 besitzt?
- Gib zu beiden Animationen den Wert für N an, bei dem der relative Fehler für den Näherungswert die 1%-Marke (0,1%-Marke) unterschreitet.
- Bestimme zu einem beliebigen Wert für N den Mittelwert aus beiden Näherungen. Berechne für diesen Mittelwert den absoluten und relativen Fehler. Vergleiche das Ergebnis mit den angezeigten Fehlerwerten in den beiden Animationen. Interpretiere das Ergebnis.
- Erstelle eine Excel-Tabelle mit den Spalten Eckenzahl N / Fläche einb.N-Eck /rel.Fehler/ Fläche umb.N-Eck / rel.Fehler/ Mittelwert einb.-umb. /rel.Fehler). Finde auf diese Weise den Wert für N, bei dem der Mittelwert der entsprechenden Vielecksflächen die 1%-Marke (0,1%-Marke) unerschreitet.

Näherung von pi mit der "Monte-Carlo Methode"
Beschießt man ein Quadrat mit der Seitenlänge 2 mit zufällig auftreffenden Punkten, dann verteilen diese sich nach dem Gesetz der großen Zahlen recht gleichlmäßig über die gesamte Fläche.
Legt man in dieses Quadrat einen Einheitskreis und zählt die Treffer darin, so ist das Verhältnis der Treffer im Kreis zu allen Treffern näherungsweise gleich dem Verhältnis von pi zur Zahl 4. (Fläche des Einheitskreises durch Quadratfläche).
Eine schöne GeoGebra-Arbeitsumgebung beschreibt, wie man mit vielen Versuchen einen ordentlichen Näherungswert für die Zahl pi erhält.