Beschränktes Wachstum

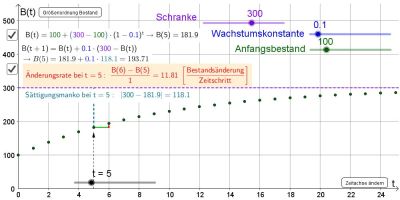
Beim beschränkten Wachstum nimmt ein Bestand ausgehend von einem Anfangsbestand stetig zu (bzw. ab) bis er sich an eine obere (bzw. untere) Grenze, die so genannte Schranke annähert. Solch eine Schranke kann beispielsweise eine maximale Höhe sein, die ein Baum oder ein anderes Lebewesen erreichen kann.

Explizite und rekursive Wachstumsformel des exponentiellen Wachstums

Wie beim linearen und exponentiellen Wachstum gibt es auch für das beschränkte Wachstum eine explizite und eine rekursive Wachstumsvorschrift. Die Behandlung der expliziten Formel ist im Lehrplan jedoch nicht vorgesehen, so dass viele SchülerInnen beim beschränkten Wachstum nur mit der rekursiven Methode arbeiten.

Für beide Formeln benötigen wir den Wert der Schranke (S) sowie den Wachstumsfaktor (k).

1. Für die explizite Berechnung des Bestandes zu einem beliebigen Zeitpunkt t müssen wir zusätzlich den Anfangsbestand (B(0)) kennen:

   B(t) = S-(S-B(0))*(1-k)^t

2. Bei der rekursiven Formel benötigen wir neben den beiden obigen Werten den aktuellen Bestand (B(t)), um den Folgebestand zu bestimmen. Die Differenz aus Schranke und aktuellem Bestand (S-B(t)) wird Sättigungsmanko genannt.

B(t+1)=B(t)+k*(S-B(t))

Animation zum grafischen Verlauf beim beschränkten Wachstum

Die Änderungsrate

Die Änderungsrate entspricht als "Bestandsänderung pro Zeitschritt" der Differenz zweier aufeinanderfolgender Bestandswerte (B(t+1)-B(t)). An der obigen rekursiven Formel erkennt man leicht die Gültigkeit des folgenden Merksatzes:

Beim beschränkten Wachstum ist die Änderungsrate proportional zum Sättigungsmanko.
Kurz: B(t+1)-B(t)=k*(S-B(t))

Hinweis:

Streng genommen handelt es sich bei der linken Seite der obigen Berechnung um eine absolute Änderung und nicht um eine Änderungsrate. Wir müssten diese Differenz eigentlich noch durch einen Zeitschritt teilen. Durch die Division durch 1 ändert allerdings nichts am Zahlenwert. Lediglich bei der Einheit erhält man durch diese Division (anstatt Bestandseinheiten) den Ausdruck "Bestandseinheiten pro Zeitschritt".