Exponentielles Wachstum / exponentieller Zerfall

Viele Prozesse, bei denen ein Bestand im Laufe der Zeit zu- oder abnimmt, lassen sich mit dem Modell des exponentiellen Wachstums beschreiben. Nimmt ein Bestand exponentiell ab, spricht man von einem exponentiellen Zerfall oder von einem exponentiellen Wachstum mit einem Wachstumsfaktor zwischen 0 und 1.

Explizite und rekursive Wachstumsformel des exponentiellen Wachstums

Die Wachstumsvorschrift (auch Wachstumsfunktion) liefert eine Berechnungsformel für den Bestand nach t Zeitschritten und hat beim exponentiellen Wachstum zwei verschiedene Formen:

1. Die explizite Darstellungsform des exponentiellen Wachstums ermöglicht die direkte Berechnung eines Bestandes nach beliebig vielen Zeitschritten:
   

   B(t)=B(0)*a ^t

   B(0) steht für den Anfangsbestand (zu Beginn der Zeitrechnung).
   Der Wert a wird als Wachstumsfaktor bezeichnet. Beachte, dass a immer positiv sein muss und in der Regel nahe bei 1 liegt (s. u.).
2. Die so genannte rekursive Darstellungsform des exponentiellen Wachstums ermöglicht nur eine schrittweise Berechnung des nächsten Bestandes mit Hilfe des vorherigen Wertes. Die rekursive Formel lautet:
   

   B(t+1) = B(t)*a

   Auch in der rekursiven Formel taucht der Wachstumsfaktor a auf.

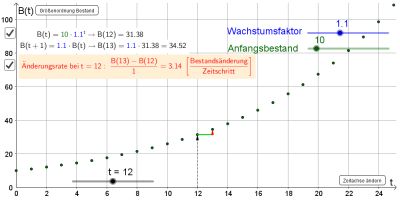
Animation zum grafischen Verlauf von exponentiellen Wachstums- und Zerfallsprozessen

Die Änderungsrate

Unter der Änderungsrate verstehen wir (in der Mittelstufe) die Bestandsänderung pro Zeitschritt.
Mit Hilfe der Animation erkennst du leicht, dass die Änderungsrate (bei exponentieller Zunahme) mit zunehmendem t immer größer wird. Hier gibt es sogar einen Zusammenhang zum jeweiligen (alten) Bestand:

Die Änderungsrate ist beim exponentiellen Wachstum stets proportional zum alten Bestand.

Die Mathematiker (und auch die Physiker) ersetzen "proportional" durch ein Gleichheitszeichen und eine Konstante. Damit wird aus dem fett gedruckten Satz:

B(t+1)-B(t)=k*B(t)

Den Wert k nennen wir Proportionalitätskonstante des exponentiellen Wachstums. Er wird oft in Prozent angegeben. (Bei Zinseszinsaufgaben ist k übrigens der Zinssatz pro Jahr).

Hinweis:

Streng genommen handelt es sich bei der linken Seite der obigen Berechnung um eine absolute Änderung und nicht um eine Änderungsrate. Wir müssten diese Differenz eigentlich noch durch einen Zeitschritt teilen. Die Division durch 1 ändert allerdings nichts am Zahlenwert. Lediglich bei der Einheit erhält man durch diese Division (anstatt Bestandseinheiten) den Ausdruck "Bestandseinheiten pro Zeitschritt".

Zusammenhang Wachstumsfaktor a und Proportionalitätskonstante k

Wir erhalten den Wachstumsfaktor a, indem wir die Proportionalitätskonstante k zu eins addieren. (Bei exponentiellen Abnahmen interpretieren wir die Zerfallskonstante als eine negative Zahl zwischen null und 1, somit muss der Wachstumsfaktor bei diesen Prozessen zwischen null und 1 liegen).

Beispiele:

1. Bei einem Zinssatz von 3,5% p. a. ist die Proportionalitätskonstante k=0,035. Die Kapitalanlage mit Zinseszins lässt sich folglich mit der Wachstumsfaktor a=1,035 beschreiben. Daraus erhalten wir die (explizite) Kapitalformel: K(t)=K₀*1,035^t.
2. Zerfallen bei einerm radioaktiven Stoff pro Jahr 0,1% der Kerne, nimmt die Stoffmenge ab. Damit ist die Proportionalitätskonstante negativ (k=-0,001). Die Formel für den Zerfallsprozess lautet: B(t)=B₀*0,999^t. (Bei einem Zerfall muss die Zerfallskonstante kleiner als 1 sein!)

Zusammenfassung wichtiger Merkmale des exponentiellen Wachstums

• Beim exponentiellen Wachstum ist die Änderungsrate zu jedem Zeitpunkt proportional zum alten Bestand.
  

  Kurz: B(t+1)-B(t)=k * B(t)

• Die Proportionalitätskonstante k darf nicht mit dem Wachstumsfaktor a verwechselt werden. a ist immer eine positive Zahl (meist nahe bei 1), während die Konstante k bei einer exponentiellen Zunahme positiv und bei einer exponentiellen Abnahme negativ ist.
  Der Wachstumsfaktor a und die Proportionalitätskonstante stehen in einem direkten Zusammenhang:

  a=1+k bzw. k=a-1

• Bei einer exponentiellen Zunahme ist der Wachstumsfaktor a immer eine Zahl größer als eins - bei einer exponentiellen Abnahme ist a<1.
• Der Wachstumsfaktor a erlaubt zum einen die Berechnung des Folgebestandes mit Hilfe des alten Bestandes:

  Kurz: B(t+1)=a * B(t) (rekursive Wachstumsformel),

  zum Anderen kannst du mit a jeden beliebigen Bestand direkt mit Hilfe des Anfangsbestandes berechnen:

  B(t)=B(0)*a^t (explizite Wachstumsformel)

• Das Schaubild einer exponentiellen Zunahme steigt (von links nach rechts betrachtet) immer steiler an (die Änderungsrate ist positiv und wird immer größer).
  Der tiefste Punkt ist der "Startpunkt" auf der B(t)-Achse mit dem Hochwert B(0).
• Das Schaubild einer exponentiellen Abnahme fällt (mit zunehmendem t) immer flacher ab (die Änderungsrate ist negativ wird betragsmäßig (!) immer kleiner). Es schmiegt sich früher oder später an die t-Achse an (ohne sie jemals zu berühren).
  Der höchste Punkt ist der "Startpunkt" auf der B(t)-Achse mit dem Hochwert B(0).