Rechengesetze
Die drei wichtigsten Rechengesetze sind das Vertauschungsgesetz (Kommutativgesetz), das Verbindungsgesetz (Assotziativgesetz) und das Verteilungsgesetz (Distributivgesetz). Wer diese Gesetze anwenden kann, hat es bei der Berechnung von Termen leichter.
Du kannst jetzt entweder den folgenden Text lesen, dir zu jedem der drei Gesetze eine Präsentation anschauen, oder gleich auf die Seite mit den Übungen gehen.
1. Das Vertauschungsgesetz - Kommutativgesetz
Präsentation zum Vertauschungsgesetz ![]()
- § In einer Summe dürfen Summanden vertauscht werden! §
13 + 7 = 7 + 13
- § In einem Produkt dürfen Faktoren vertauscht werden! §
4 · 5 = 5 · 4
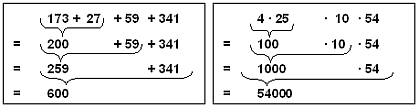
Durch geschicktes Vertauschen kann die Berechnung der beiden Terme vereinfacht werden:
Summe : 341 + 173 + 59 + 27 |
Produkt: 4 · 54 · 10 · 25 |
2. Das Verbindungsgesetz -Assoziativgestz
Präsentation zum Verbindungsgesetz ![]()
- § In einer Summe dürfen Klammern beliebig gesetzt oder weggelassen werden! §
13 + 14 + 17 + 16 = (13 + 17) + (14 + 16) = 30 + 30
- § In einem Produkt dürfen Klammern beliebig gesetzt oder weggelassen werden! §
4 · 5 · 25 · 20 = (4 · 25) · (5 · 20) = 100 · 100
Dadurch wird die Berechnung der beiden Terme noch einfacher: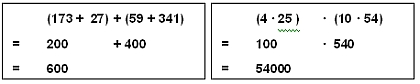
3. Das Verteilungsgesetz - Distributivgesetz
Präsentation zum Verteilungsgesetz ![]()
Das Verteilungsgesetz gilt, wenn Punkt- und Strichrechnungen in bestimmten Kombinationen vorkommen. In den folgenden Beispielen wird das Verteilungsgesetz nur für die Addition in Verbindung mit der Multiplikation verwendet.
a) Ausmultiplizieren
Multipliziert man eine Summe (z.B. 50 + 6) mit einer Zahl ( z.B. 3), dann kann man auch jeden Summanden in der Klammer mit dieser Zahl multiplizieren und die Produkte addieren.![]()
b.) Ausklammern
Umgekeht gilt : Kommt in einer Summe aus Produkten ein gemeinsamer Faktor vor, darf man diesen auch ausklammern.![]()
Das Verteilungsgesetz gilt auch für:
Multiplikation von Differenzen Bsp.: 4 · (15 - 6) = 4 · 15 - 4 · 6
Division von Summen Bsp.: (15 + 6) : 3 = 15 : 3 + 6 : 3
Division von Differenzen Bsp.: (15 - 6) : 3 = 15 : 3 - 6 : 3
Hier geht es zu einem Beispiel für die Anwendung des Verteilungsgesetzes bei der Addition von Pfeilen.
Herausgeber: Landesbildungsserver Baden-Württemberg
Quelle: https://www.schule-bw.de
Bitte beachten Sie eventuell abweichende Lizenzangaben bei den eingebundenen Bildern und anderen Dateien.



