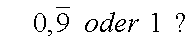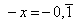Welche Zahl ist größer?

Hintergrund:
Die obige E-Mail Anfrage gab Anlass zu einer online- Recherche, verbunden mit einer etwas erweiterten Antwort.

Didaktischer Ort:
Man könnte diese Frage jederzeit auch im Unterricht stellen und die Schülerinnen und Schüler zu eigenen Recherchen anhalten. Aus den angedeuteten Antworten leitet man leicht ab, dass JEDE Klassenstufe der weiterführenden Schulen an dieser Frage Interesse finden kann.

Ergebnis vorab:
Die beiden Darstellungen bezeichnen die gleiche Zahl, haben also den gleichen Wert. Deshalb ist keine der beiden größer.

Beleg für die Sekundarstufe 1:

Division durch Neun

Durch einfache schriftliche Division erhält man 3 : 9 = 0,33333... oder
.

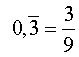Entsprechend findet man 6 : 9 = 0,66666... oder

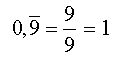
Logischerweise ergibt sich dann

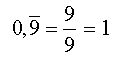
Beschreibend

Wir betrachten die beiden Zahlen

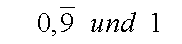
_{in der Schreibweise mit Kommata und subtrahieren beiden von einander:}

1,00000...0

0,00000...1?

Es ist klar, dass in der Differenz die ersten Ziffern alle Null sind. Umgangssprachlich wäre aber die letzte Ziffer (und nur die letzte Ziffer!) eine Eins.
Tatsächlich gibt es aber keine letzte Ziffer! Folglich sind alle Ziffern der Differenz Null. Hieraus wird deutlich, dass sich die beiden Zahlen nicht unterscheiden.

Multiplikation und Subtraktion

Es gilt:
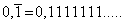(1)
Wir bezeichnen die linke Seite mit x, dann gilt
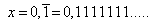(2)
Multipliziert man die Gleichung mit dem Faktor 10, so ergibt sich links und rechts das Zehnfache, nämlich:
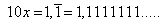(3)

Zieht man nun die Gleichung (2) von der Gleichung (3) ab, so erhält man:

____________________

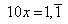
9x = 1 (4)

Aus dieser vierten Gleichung folgt x=1/9.

Durch Analogieschluss ergibt sich:

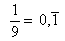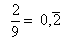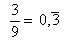, , , usw. bis

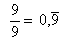
Damit ist die Eingangsfrage beantwortet.

ODER DOCH NICHT???

Darf man denn periodische Dezimalbrüche in der vorgegebenen Art multiplizieren oder subtrahieren?
Das ist jedenfalls NOCH NICHT bewiesen!

Beleg für Sekundarstufe 2

Folgen

Wir betrachten die Folge

0,9
0,99
0,999
0,9999
....

Man erkennt unschwer, dass die Folge gegen eine Zahl der Form 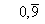konvergiert, andererseits aber sicherlich auch den Grenzwert 1 ein.
Man betrachte den Abstand (Differenz) jedes Folgeglieds zu 1: er ergibt sich eine Nullfolge.

Exkurs:
Zu jedem Epsilon>0 findet man ein Folgeglied n₀, so dass alle auf n_o folgenden Glieder vom Grenzwert 1 weniger als Epsilon entfernt sind.

Da die Folge einen eindeutigen Grenzwert besitzt, muss 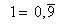gelten.

Reihe

Man kann die Zahl 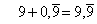auch als (unendliche) Reihe darstellen.

Dann gilt sicherlich

(5)

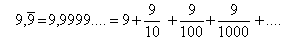
Die rechte Seite der Gleichung stellt aber eine geometrische Reihe in der Form

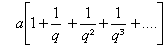dar, die bekanntlich den Summenwert 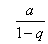besitzt, solange IqI<1 ist.

In unserem Falle ist a=9 und q=1/10 .

Damit ist die Summe der obigen geometrischen Reihe

(6)

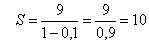
Aus den Gleichungen (5) und (6) folgt wiederum die zu Beginn erstellte Behauptung.

Online- Quellen

Etwas abseits liegend , aber durchaus auch für Informatikkurse interessant, ist der folgende Artikel über Gleitkommazahlen und Rundungsfehler:

http://www.dreael.ch/Deutsch/BASIC-Knowhow-Ecke/Gleitkommazahlen.html