Animation zu den Kennwerten von Boxplots
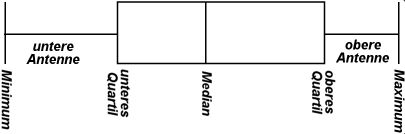
Beispiel: Körpergrößen in verschiedenen Klassenstufen
Erfrage in deiner Schule in verschiedenen Klassenstufen die Körpergrößen der Schülerinnen und Schüler und notiere diese für jede Klassenstufe in einer Datenliste. Vermutlich werden die Körpergrößen mehr oder weniger stark voneinander abweichen.
Mit Boxplots kannst du in wenigen Schritten die Datensätze der Klassen so aufarbeiten, dass man sofort erkennt, wie stark die jeweiligen Daten "gestreut" sind.
- Im ersten Schritt müssen die Daten der Größe nach sortiert werden.
- Die äußeren Ränder des Boxplots sind durch den kleinsten Wert der Datenreihe (das Minimum) und den größten Wert (das Maximum) festgelegt. Der Abstand dieser beiden Punkte heißt Spannweite der Verteilung.
-
Bei einer ungeraden Anzahl von Daten heißt der Wert in der Mitte Median (Zentralwert). Er wird häufig mit xMed abgekürzt und teilt die Datenliste exakt in zwei Hälften.
Bei einer geraden Anzahl von Daten findest du den Median, indem du das arithmetische Mittel der beiden mittleren Werte berechnest. (Arithmetisches Mittel zweier Zahlen = die Hälfte der Summe dieser beiden Zahlen). - Die "Box" soll so groß gezeichnet werden, dass sich darin mindestens 50% der Daten befinden. Hierzu bestimmen wir den Median der unteren Hälfte, das so genannte untere Quartil und den Median der oberen Hälfte, das so genante obere Quartil.
Wenn eines dieser Quartile zwischen zwei Listenwerte liegt, berechne einfach wieder das zugehörige arithmetische Mittel der benachbarten Listeneinträge. - Mit Hilfe der drei mittleren Werte (unteres Quartil, Median, oberes Quartil) kannst du nun die Box zeichnen. Verlängere sie auf beiden Seiten bis zum Minimum bzw. bis zum Maximum. Diese beiden Linien bezeichnet man als "Antennen" oder auch als "Whisker" (engl. für Schnurrhaar).
Liegt ein Wert (oder mehrere) mehr als das 1,5-fache der Boxenbreite von der Box entfernt, so werden diese Zahlen gelegentlich als "Ausreißer" durch Punkte markiert. Die jeweilige Antenne verkürzt sich dann von der Box bis zum nächstgrößeren bzw. nächstkleineren Wert.
Hinweise zur nachfolgenden Animation
- Die x-Werte der blauen Punkte liefern je einen Zahlenwert. Mit der Maus kannst du die Punkte horizontal verschieben und dadurch das Aussehen des Boxplots verändern.
- Mit dem Schieberegler für n kannst du die Anzahl der Punkte verändern.
- Ausreißer werden nur als Punkte markiert, wenn dies mit einem Haken im zugehörigen Auswahlfeld gefordert wird.
- Mit dem Pfeilsymbol oben rechts kannst du die Animation in ihren Anfangszustand zurück versetzen. Alternativ funktioniert dies auch durch Drücken der F5-Taste.
Aufgaben zur Animation
- Verändere mit der Maus die Lage der Punkte und überlege, ob, warum und an welcher Stelle sich der Boxplot dabei verändert.
- In welchen Fällen liegt der Median genau bei dem x-Wert eines Punktes?
- In welchen Fällen liegt das untere Quartil genau zwischen den x-Werten zweier benachbarter Punkte?
- Konstruiere einen Fall, bei dem das untere Quartil genau einem x-Wert der Liste entspricht, das obere Quartil jedoch in der Mitte zwischen zwei benachbarten Listenwerten liegt.
- Starte die Animation mit der F5-Taste neu, setze den Haken bei "Ausreißer anzeigen" und verändere den Schieberegler. Warum wird der maximale Wert z. B. bei n=14 nicht als Ausreißer markiert?
- Welche Mindestanzahl an Einträgen muss die Liste besitzen, damit ein Randwert überhaupt als Ausreißer dargestellt werden kann?
Linktipp:
Der nachfolgende Link führt zu einer Anleitung für die Boxplot-Bestimmung mit dem wissenschaftlichen Taschenrechner (WTR).
Das Dokument beinhaltet darüber hinaus eine Übungsaufgabe mit Daten zur Fußball-Bundesliga.



