Daten auswerten
Um Daten zu interpretieren und miteinander zu vergleichen verwendet man Kennwerte. Fünf dieser Kennwerte sind die Grundlage für Boxplots (Kastendiagramme), die die Verteilung von Daten grafisch veranschaulichen.
Kennwerte
Statistische Untersuchungen haben meist das Ziel, Informationen über bestimmte Eigenschaften einer Gruppe von Personen oder Objekten zu erhalten. In einer Untersuchung (Stichprobe) ermittelt man Daten, die dazu geeignet sind, Aussagen über diese Eigenschaften zu treffen. Dabei spielen statistische Kennwerte eine wichtige Rolle. Am Beispiel der Klassenarbeitsnoten zweier Parallelklassen werden folgende
Kennwerte näher erläutert:
- Minimum
- Maximum
- Spannweite
- Arithmetisches Mittel (Durchschnitt)
- Zentralwert (Median)
- Quartile
- 1. Quartil (unteres Quartil qu)
- 2. Quartil (mittleres Quartil / Median)
- 3. Quartil (oberes Quartil qo)
Boxplots
Boxplots sind grafische Veranschaulichungen (Kastenschaubilder oder Kastendiagramme), die die Verteilung der Daten einer Rangliste darstellen.
Das Diagramm wird aus 5 Kennwerten eines Datensatzes (Beispiel: Minimum = 1, Maximum = 5,5, qu = 1,9 , qo = 3,7 und dem Zentralwert = 2,9) erstellt.
Beispiel 1: Boxplot zur Verteilung der Noten der Klasse 7a
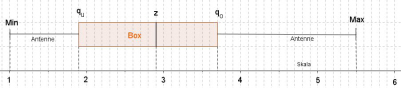
In Beispiel 1 beträgt der Notendurchschnitt 2,8. Der Zentralwert liegt bei 2,9.
Es gab Noten von 1,0 bis 5,5. Die Spannweite ( Differenz zwischen Maximum und Minimum) ist 4,5.
Die Box veranschaulicht den Bereich, in dem die mittleren 50 % der Daten liegen. Sie wird durch das obere und das untere Quartil begrenzt.
Der Zentralwert (Median) wird als durchgehender Strich in der Box eingezeichnet. Dieser Strich teilt das gesamte Diagramm in zwei Hälften, in denen jeweils 50 % der Daten liegen.
Beispiel 2: Boxplot zur Verteilung der Noten der Klasse 7b

In Beispiel 2 beträgt der Notendurchschnitt ebenfalls 2,8. Der Zentralwert liegt bei 2,7.
Es gab Noten von 1,5 bis 6,0. Die Spannweite ist ebenfalls 4,5.
Die Box, in der die mittleren 50 % der Daten liegen, ist hier kleiner.
Zusammenfassung der Inhalte als Präsentation
Weitere anschauliche Beispiele zur Erstellung von Boxplots findet man unter: Beispiel 1 und Beispiel 2



