Grundbegriffe
Daten und Zufall
Eine Aufgabe der Wahrscheinlichkeitsrechnung ist die Untersuchung von Vorgängen, deren Ausgang unvorhersagbar also zufällig ist. Ziel dieser Untersuchung ist es, mögliche Gesetzmäßigkeiten für Voraussagen zu finden. Die Grundlage dafür bilden Zufallsexperimente (Zufallsversuche). Diese können mit unterschiedlichen Zufallsgeräten durchgeführt werden. Am Beispiel „Würfeln“ werden im Folgenden die wichtigsten Grundbegriffe erklärt.
Grundbegriffe
1. Das einstufige Zufallsexperiment „Würfeln mit einem Würfel“
Ein Zufallsexperiment hat folgenden Eigenschaften:
- Es ist unter gleichen Bedingungen beliebig oft wiederholbar
- Es gibt mindestens zwei mögliche Ergebnisse
- Das Ergebnis ist nicht vorhersagbar
Weitere Beispiele für Zufallsexperimente:
Werfen einer Münze – Würfeln mit einem Würfel – Würfeln mit einem beliebigen Körper ( Quader,Tetraeder, Oktaeder, …) – Entnehmen einer Kugel aus einem Gefäß – Ziehen einer Spielkarte - Schere/Stein/Papier – Drehen eines Glücksrades – Umfrage
2. Ergebnis / Ergebnismenge - Ereignis
Ein Zufallsexperiment hat eine bestimmte Anzahl an möglichen Ergebnissen (Ausgängen). Beim Würfeln mit einem Würfel sind es genau sechs Ergebnisse, die eintreten können. Diese kann man in der Ergebnismenge S = {1;2;3;4;5;6} zusammenfassen. Ein Ereignis fasst in der Regel mehrere Ergebnisse zusammen. Präziser ausgedrückt: Ein Ereignis ist eine Teilmenge der Ergebnismenge. Auch S selbst ( das sichere Ereignis) und die leere Menge ( das unmögliche Ereignis) sind Teilmengen von S.
Oft kürzt man Ereignisse mit großen Buchstaben ab. Soll das Ergebnis eines Wurfs eine Gerade Zahl sein, so wird dies durch die 3 Ergebnisse das Ereignis A = {2; 4; 6} erfüllt.
Bsp: Mehrere Ergebnisse werden zu einem Ereignis zusammengefasst :
Beispiele für Ereignisse:
| Das Ereignis.. | ..besteht aus den Ergebnissen |
| (A) Gerade Zahl | (A) = { 2;4;6} |
| (B) Ungerade Zahl | (B) = { 1;3;5} |
| (C) „Kleiner als 5“ | (C) = { 1;2;3;4} |
| (D)„Größer als 1“ | (D) = { 2;3;4;5;6} |
| (E)„Größer als 6“ | (E) = { } |
Besondere Ereignisse:
a) Das sichere Ereignis
z.B. " Die gewürfelte Zahl ist eine natürliche Zahl"
b) Das unmögliche Ereignis
Das letzte Beispiel in der Tabelle 1 zeigt das unmögliche Ereignis z.B. eine 7 zu würfeln.
c) Zu jedem Ereignis gibt es ein Gegenereignis
| Das Ereignis | hat als Gegenereignis |
| "Gerade Zahl" A = { 2;4;6} | "Ungerade Zahl" A´ = { 1;3;5} |
| „1“ B = { 1 } | "keine 1“ B´ ={ 2;3;4;5;6} |
| „Kleiner als 5“ C = { 1;2;3;4} | „größer als 4“ C´ = { 5;6 } |
3. Diagramme
Die Ergebnisse von Zufallsexperimenten kann man auf verschiedene Arten darstellen. Markus hat 30-mal mit einem Würfel gewürfelt und die Ergebnisse seiner Zufallsexperimente folgendermaßen dargestellt:
a.) Strichliste
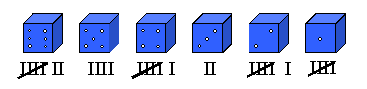
b.) Tabelle
| Ereignis | 1 | 2 | 3 | 4 | 5 | 6 |
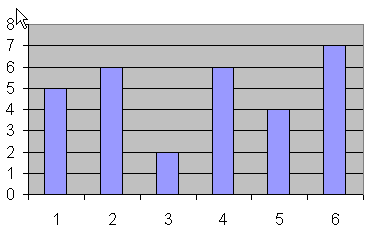
| Absolute Häufigkeit | 5 | 6 | 2 | 6 | 4 | 7 |
c.) Säulendiagramm
d.) Kreisdiagramm
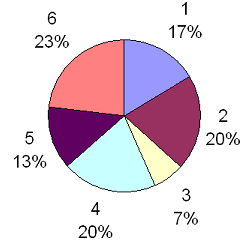
Relative und absolute Häufigkeit:
Das Kreisdiagramm zeigt, dass die Eins mit einer relativen Häufigkeit von 17% gewürfelt wurde. Die Anzahl der Versuche wurde dabei mitberücksichtigt. Es ist leicht einzusehen, dass man unterscheiden muss, ob sich die absolute Häufigkeit auf 10, 20 oder 100 Versuche bezieht. Wird die Eins bei 30 Versuchen 5 mal gewürfelt, so beträgt die relative Häufigkeit 5 von 30 = 5/30 oder 0,166.. oder gerundet 17/100 = 17%
4. Der Begriff Wahrscheinlichkeit, Laplace-Experiment
Wahrscheinlichkeiten beziehen sich immer auf ein Ereignis - und nicht auf ein Ergebnis. Möchte man die Wahrscheinlichkeit für das Würfeln einer 6 bestimmen, spricht man daher von der Wahrscheinlichkeit, dass das "Elementarereignis A={6} eintritt"
Selbst wenn wir die exakten Wahrscheinlichkeiten für das Eintreten der einzelnen Augenzahlen beim Würfeln nicht kennen, können wir davon ausgehen, dass sie für alle Zahlen gleich sind, da die Symmetrie und die Form des Würfels keine der sechs Zahlen bevorzugt. Die Wahrscheinlichkeit, eine der 6 Zahlen zu würfeln, ist für jede einzelne Zahl gleich. Diese Information reicht aus, um konkrete Aussagen über das Eintreten eines Ereignisses zu machen. Ein Zufallsexperiment, bei dem alle Elementarereignisse gleich wahrscheinlich sind, nennt man Laplace-Experiment. Für die Wahrscheinlichkeit P (A) eines Ereignisses A bei einem Laplace-Experiment gilt:

In unserem Fall gilt für die Wahrscheinlichkeit des Ereignisses (A) eine Fünf zu würfeln :
P (A) = 1/6
Hinweis: Ein Würfel ist niemals absolut symmetriesch, daher ist das Würfeln auch nur in "guter Näherung" ein Laplace-Experiment.
Bei einem "gezinkten" Würfel müsste man die exakte Wahrscheinlichkeiten für die sechs Elementarereignisse über das Protokollieren von sehr sehr vielen Würfen gewinnen. Nach dem "empirischen Gesetz der großen Zahlen", pendeln sich die relativen Häufigkeiten bei vielen Durchführungen des Zufallsexperiments bei einem Wert ein.
Das Baumdiagramm:
Das Baumdiagramm zeigt, mit welcher Wahrscheinlichkeit, die einzelnen Elementarereignisse eintreten können:
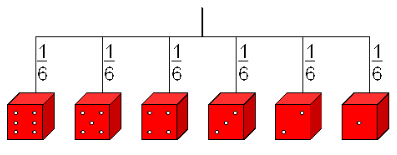
5. Summenregel
| Die Wahrscheinlichkeit eines Ereignisses ist die Summe der Wahrscheinlichkeiten der zugehörigen Elementarereignisse. |
So ergibt sich für die Wahrscheinlichkeit, eine gerade Zahl, also 2 ; 4 oder 6 zu würfeln, mithilfe der Laplace Formel folgendes Ergebnis:
Anzahl der günstigen Ergebnisse = 3
dividiert durch die
Anzahl der möglichen Ergebnisse = 6
Wahrscheinlichkeit: 3/6 = 1/2
Mithilfe der Summenregel:
Die Wahrscheinlichkeit eine 2 zu würfeln = 1/6
Die Wahrscheinlichkeit eine 4 zu würfeln = 1/6
Die Wahrscheinlichkeit eine 6 zu würfeln = 1/6
Wahrscheinlichkeit : 1/6+1/6+1/6 = 3/6 = 1/2
6. Pfadregel - Produktregel für mehrstufige Zufallsexperimente
Zufallsexperimente bestehen oft aus einer bestimmten Anzahl von Teilexperimenten, die hintereinander ausgeführt werden. Die Ermittlung von Wahrscheinlichkeiten in solchen Fällen kann recht schnell unübersichtlich werden. Hilfe bietet dabei die grafische Darstellung mit einem Baumdiagramm.
In einem Baumdiagram werden die Ausgänge eines Zufallsexperiments als Linien dargestellt und die entsprechenden Wahrscheinlichkeiten dazu geschrieben. Erweitern wir das obige Beispiel auf das zweimalige Würfeln mit der Fragestellung: „Wie groß ist dabei die Wahrscheinlichkeit 2 mal hintereinander eine Sechs zu würfeln?“ Würden wir alle möglichen Ereignisse darstellen, wird der Baum recht unübersichtlich. Da uns nur die Wahrscheinlichkeit des Ergebnisses "Sechs" interessiert, fassen wir die übrigen Ergebnisse als Gegenereignis "keine Sechs" zusammen. Der Ereignisbaum bleibt übersichtlich.
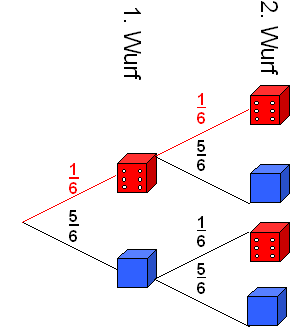
Ermittelt man Wahrscheinlichkeiten für die vier möglichen Ergebnisse nach zweimaligem Würfeln, ergibt sich folgende Regel:
Pfadregel - Produktregel
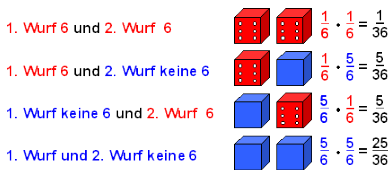
Die Wahrscheinlichkeit eines Elementarereignisses in einem mehrstufigen Zufallsversuch ist gleich dem Produkt der Wahrscheinlichkeiten entlang dem zugehörigen Pfad.
Summen und Produktregel
Möchte man bei einem mehrstufigen Zufallsexperiment die Wahrscheinlichkeit für ein Ereignis bestimmen, welches mehrere Ergebnisse zusammenfasst, so berechnet man zunächst nach der Produktregel die Wahrscheinlichkeiten für die (günstigen) Elementarereignisse und addiert diese zur Gesamtwahrscheinlichkeit.
Beispiel:
Ereignis B: "Genau ein Wurf von zweien ist eine Sechs."
Elementarwahrscheinlichkeiten (s. o.) 5/36 für die Sechs im ersten Wurf bei einer Niete im zweiten. Den gleichen Wert errechnit man bei der umgekehrten Reihenfolge.
Beide Elementarereignisse sind "günstig" für das Ereignis B. Somit gilt P(B)=5/36 + 5/36 = 5/18.
Die Wahrscheinlichkeit P(B) ist gleich der Summe der Wahrscheinlichkeiten aller Pfade, die zu einem Ergebnis von B führen.
Beispiel: Würfeln mit zwei Würfel
Herausgeber: Landesbildungsserver Baden-Württemberg
Quelle: https://www.schule-bw.de
Bitte beachten Sie eventuell abweichende Lizenzangaben bei den eingebundenen Bildern und anderen Dateien.



