Von der Funktion zur Ableitungsfunktion (Steigungsfunktion)
Hinweise zur Animation (unten):
- Der erste Start der Animation benötigt etwas Zeit.
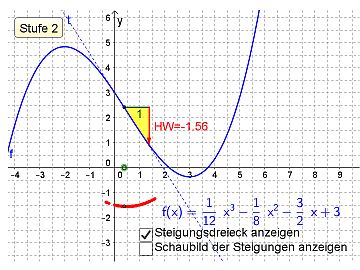
- Verändere mit der Maus die Position des grünen Kreises auf der x-Achse. Hierdurch kannst du die Lage des Punktes auf dem blauen Schaubild verändern. Es erscheint ein roter Punkt, dessen y-Wert die jeweilige Steigung des blauen Schaubildes beschreibt.
Fragen:
- Welche (beiden) Besonderheiten treten auf, wenn das „Steigungsschaubild“ die x-Achse schneidet? Begründe beide Fälle mit dem Steigungsbegriff.
- Welche Besonderheit tritt auf, wenn das Steigungsschaubild die x-Achse nur berührt (Stufe 3)? Begründe wieder mit dem Steigungsbegriff.
- Bestimme bei den Stufen 1-4 den Grad der zugehörigen Steigungsfunktion. Vergleiche jeweils mit dem Funktionsgrad des blauen Schaubildes.
- Stufe 1-7: Um welche Funktionstypen handelt es sich bei den blauen und roten Schaubildern?
Zusatzaufgabe:
Vielleicht kannst du schon ableiten. Leite die Funktion zum blauen Schaubild ab. Du kannst deine Rechnungen überprüfen, indem du die Funktionsterme in die Eingabezeile eingibst und mit Enter bestätigst. (Die Eingabezeile lässt sich leider aus technischen Gründen nicht im Browser anzeigen. Lade hierzu die unten zum Download angebotene GeoGebra-Datei auf deinen Rechner und starte sie.
Zum Ableiten bei den Stufen 6-8 benötigst du die Kettenregel (Kursstufe).



