Differenzialrechnung

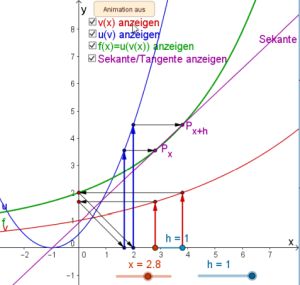
Von der Sekante zur Tangente

Wir wollen eine Tangente in einem Kurvenpunkt an das Schaubild einer Funktion legen. Dieses Problem kann - wie aus der Geometrie der Mittelstufe bekannt - als Suche nach der Grenzlage von Sekanten aufgefasst werden.

Die Animation unter dem nachfolgenden Link veranschaulicht die Vorgehensweise: die Sekantensteigung wird hierbei durch den Differenzenquotienten mit der h-Methode dargestellt. Die Animation beinhaltet verschiedene Funktionstypen - auch nicht differenzierbare Funktionen.

Animation: Von der Sekante zur Tangenten

Von der Funktion zur Ableitungsfunktion

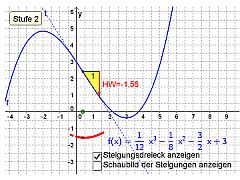
Eine mehrstufige GeoGebra-Animation ermöglicht die Entdeckung des Zusammenhangs zwischen Funktion und Ableitungsfunktion. Beiläufig werden hierbei wichtige Funktionstypen aus der Mittelstufe wiederholt.

Einsatzmöglichkeiten:

• Nachdem der Ableitungsbegriff eingeführt wurde, haben die Schüler bereits die Ableitungsregeln für ganzrationale Funktionen kennen gelernt. In diesem Fall wird mit der Animation der Zusammenhang zwischen Tangentensteigung und den Funktionswerten der Ableitungsfunktion wiederholt.
• Die Schüler kennen den Ableitungsbegriff als Steigung der Tangenten. Der Lehrer gibt die Ableitunsregel für ganzrationale Funktionen vor ohne auf deren Bedeutung einzugehen. Mit Hilfe der Animation entdecken die Schüler den Zusammenhang zwischen Ableitungsfunktion und Tangentensteigung. (Zur Eingabe von Funktionstermen muss die Animations-Datei zuvor herunter geladen und mit GeoGebra gestartet werden).
• Die Schüler bestimmen die Ableitungsfunktion als Funktion zur Ortskurve der Tangentensteigungen. Hierbei wiederholen sie, wie man zu einer Geraden (Parabel ) eine lineare (quadratische) Funktion bestimmt. Die Ableitungsregeln werden erst später eingeführt.

Mehrstufige GeoGebra-Animation mit Fragen und Arbeitsaufträgen

Tangenten- und Normalengleichung

Umfangreiche Lernumgebung mit Lernvideos, Animationen und Übungsaufgaben zum Thema

Ausgehend von der Suche nach Tangenten am Kreis können wir die Tangentenbestimmung bei Schaubildern in zwei Typen einteilen:

1. Ein Punkt ist auf dem Schaubild gegeben (z. B. ein Wendepunkt). Es ist die zugehörige Tangente gesucht. Wie findet man die Gleichung?
2. Nur etwas komplizierter ist die Suche nach einer Tangentengleichung beim Typ 2, wenn der Tangentenberührpunkt (bzw. die Tangentenberührpunkte) nicht gegeben ist (sind).

Neben mehreren Lernvideos finden Sie in der Lernumgebung auch animierte Übungsaufgaben mit Lösungen - zum Teil mit Lernvideo.

Zur Lernumgebung Tangenten- und Normalengleichungen

Informationen aus dem Schaubild der Ableitungsfunktion

Die hier vorgestellte Geogebra-Animation verdeutlicht den Zusammenhang zwischen Ableitungsfunktion und zugehöriger Stammfunktion.

Kurzbeschreibung:

• Bei angezeigter Stammfunktion erkennen sie, dass sich alle Funktionen mit gleicher Ableitungsfunktion nur durch einen konstanten Summanden unterscheiden.
• Auch das Schaubild der Ableitungsfunktion kann mit einem Schieberegler in y-Richtung verschoben werden. Hierbei werden die Veränderungen bei der angezeigten Stammfunktion augenblicklich angezeigt.
• Mit Hilfe der Animation lassen sich das notwendige und das (erste) hinreichende Kriterium für Extremstellen sehr schön veranschaulichen. Darüber hinaus erkennen sie einen Zusammenhang zwischen den Extremstellen der Ableitungsfunktion und den Wendestellen der Stammfunktion.
• Aufgaben ermöglichen einen experimentellen Zugang zum Thema und sichern den Lernerfolg.

Auch hier benötigen Sie zur Anzeige Java 1.4 oder höher.

Informationen aus dem Schaubild der zweiten Ableitungsfunktion

Ähnlich wie die obige Animation verdeutlicht diese Geogebra-Animation den Zusammenhang zwischen der zweiten Ableitungsfunktion und einer zugehörigen Stammfunktion.

Kurzbeschreibung:

• Bei angezeigter Stammfunktion lässt sich erschließen, dass sich alle Funktionen mit gleicher zweiter Ableitung höchstens durch einen linearen und/oder konstanten Summanden unterscheiden.
• Wiederum lässt sich das Schaubild der Ableitungsfunktion mit einem Schieberegler in y-Richtung verschieben. Hierbei werden die Veränderungen bei der angezeigten Stammfunktion augenblicklich angezeigt.
• Mit Hilfe der Animation lässt sich der Krümmumgsbegriff sehr schön darstellen. Ebenso finden sie Kriterien für Extrem- und Wendestellen.
• Aufgaben ermöglichen einen experimentellen Zugang zum Thema und sichern den Lernerfolg.

Auch hier benötigen Sie zur Anzeige Java 1.4 oder höher.

Verkettung von Funktionen - Animation und Fragestellungen zur Kettenregel

Die Schaubilder von verketteten Funktionen können mit Hilfe der Schaubilder zur inneren und äußeren Funktion nur schwer erschlossen werden. Die hier vorgestellte Animation ermöglicht ein dynamisches Verständnis und bietet einen experimentellen Zugang zu diesem Themenbereich.

Die Seite beinhaltet eine schrittweise Anleitung, mit deren Hilfe sich Schülerinnen und Schüler selbstständig die Ableitungsregel von verketteten Funktionen erarbeiten können.

Herleitung der Produktregel

Mit Hilfe einer Prezi-Präsentation wird die zentrale Beweisidee sowie die wesentlichen Schritte bei der Herleitung der Produktregel vorgeführt. Die Präsentation beinhaltet auch eine Wiederholung der Ableitungsdefinition sowie verschiedene Beispiele.

Kurvendiskussion

Das Newton-Verfahren

Bei der Kurvendiskussion führen die notwendigen Bedingungen für Extremstellen und Wendestellen auf die Problematik der Nullstellenbestimmung. Da es nicht für alle Gleichungstypen Lösungsformeln gibt, ist es ohne Taschenrechner unter Umständen sinnvoll, die Newton-Formel für die Nullstellenbestimmung zu verwenden. Wenn auch in Zeiten von GTR und CAS veraltet, so liefert sie uns noch immer eine gute Möglichkeit, unser Wissen über die Differenzialrechnung zu vertiefen. Weitere Informationen, Fragestellungen, ein Arbeitsblatt und eine Animation zum Prinzip des Newton-Verfahrens finden Sie hier:

Materialien zum Thema Funktionenschar (Parameterfunktion)

In einer umfangreichen Lernumgebung zum Thema Funktionenschar mit vielen Animationen und Lernvideos wird das notwendige Wissen zum Lösen von Abituraufgaben schülergerecht dargestellt.

Funktionenscharen (Parameterfunktionen)

Differenzialgleichungen bei exponentiellem und beschränktem Wachstum

Eine Differenzialgleichung (DGL) ist eine Gleichung, bei der eine (gesuchte) Funktion und deren Ableitungsfunktion auftreten. Im Gegensatz zu "normalen" Gleichungen wird eine DGL durch Funktionen gelöst. Beim exponentiellen Wachstum findet man die gesuchte Bestandsfunktion recht einfach durch Aufleiten. Beim beschränkten Wachstum benutzt man die Technik der Substitution. Wie das bei Funktionen funktioniert sehen Sie im folgenden Dokument, das sowohl im OpenOffice, als auch im PDF-Format vorliegt.

Vergrößern

Differenzialgleichungen bei exp. und beschr. Wachstum als OpenOffice-Datei Download
Dokument als PDF Download

Zum Seitenanfang