Tangenten- und Normalengleichungen

Tangenten- und Normalengleichungen lassen sich in der "Punkt-Steigungs-Form leicht ineinander überführen. Ist die Steigung der Tangenten bekannt, so folgt die Steigung der zugehörigen Normalen indem man den negativen Kehrwert der Tangentensteigung bildet. Umgekehrt verhält es ich natürlich genauso. Dies ist die Aussage der Tangenten-Normalenbeziehung (Orthogonalitätsbeziehung) m_t*m_n=-1 bzw. m_n=-1/m_t.
Beispiel: Ist die Steigung der Tangenten in einem Punkt P m_t=3/4, so beträgt die Steigung der Normalen im Punkt P m_n=-4/3. (Siehe Lernvideo Punkt-Steigungs-Form der Tangenten- und Normalengleichung).

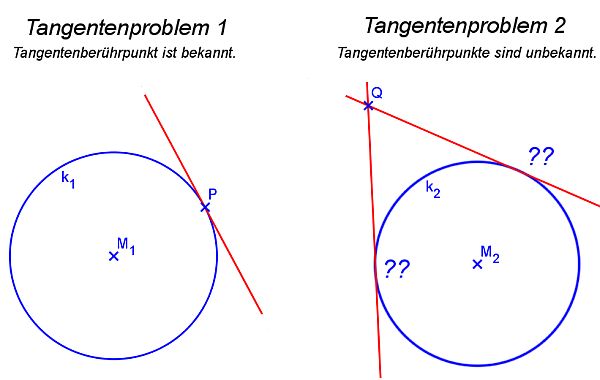
Die zwei Grundprobleme bei der Suche nach Tangenten

Wir vergleichen die Suche nach Tangenten an Schaubildern mit der Suche nach Tangenten beim Kreis. Du kennst in diesem Zusammenhang aus der Mittelstufe vielleicht noch die folgenden Grundaufgaben:

1. Gegeben ist ein Kreis k₁ und ein Punkt P auf der Kreislinie. Konstruiere die Tangente an den Kreis durch P.
2. Gegeben ist ein Kreis k₂ und ein Punkt Q außerhalb des Kreises. Konstruiere die Tangente(n) an den Kreis durch Q.

Ausgehend von diesen beiden Fragestellungen sprechen wir im Folgenden von zwei "Tangentenproblemen".

Tangentengleichungen aufstellen

Typ 1: mit bekanntem Tangentenberührpunkt - mit Lernvideo

Ein Punkt auf dem Schaubild ist gegeben. Verwerte die Koordinaten des gegebenen Punktes und bestimme mit Hilfe der ersten Ableitung die Steigung der gesuchten Tangenten.

Bei unserem Lernvideo zu diesem Thema ist die Wendetangente gesucht. Hierfür wird zunächst der Wendepunkt berechnet (bis 1:50 Min.). Du kannst diese Passage problemlos überspringen.

Zum Lernvideo Typ 1: Tangentengleichung aufstellen bei bekanntem Tangentenberührpunkt

Typ 2: unbekannte Tangentenberührpunkte - mit Lernvideo

Hier ist in der Regel ein Punkt außerhalb des Schaubildes gegeben, wobei der Berührpunkt der gesuchten Tangenten nicht bekannt ist.

Da die Koordinaten des Berührpunktes direkt in die Tangentengleichung eingehen, musst du zunächst den (die) Berührpunkt(e) bestimmen (meist gibt es mehrere Berührpunkte und somit dann auch mehrere Tangenten). Hierfür werden die Koordinaten des gegebenen Tangentenpunktes verwendet. Dies führt auf eine Bestimmunggleichung für den x-Wert des Berührpunktes (der Berührpunkte).

Zum Lernvideo Typ 2: Tangentengleichung aufstellen bei unbekannten Tangentenberührpunkten

Dynamische Animation: Tangenten durch einen Punkt außerhalb des Schaubildes (Tangentenproblem Typ 2)

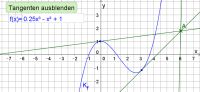
Bei der Animation kann das Schaubild mit der Maus verschoben werden Alternativ kann die Animation durch Eingabe eines neuen Funktionsterms nahezug beliebig auf anderer Situationen (Aufgabenstellungen) angepasst werden. Auch der Tangentenpunkt außerhalb des Schaubildes lässt sich mit der Maus verändern.

Schnell erkennt man, bei welchen Schaubildern und für welche Punkte es besonders viele bzw. besonders wenige Tangenten gibt.

Geogegra-Animation Tangenten durch einen Punkt außerhalb des Schaubildes (Tangentenproblem Typ 2)

"Tangenten-Probleme" in der Oberstufe

Zusammenfassung der Problemstellungen mit möglichen Lösungswegen

Sehr viele Abituraufgaben laufen darauf hinaus, dass eine Tangente an ein Schaubild in der Form bestimmt werden muss, dass sie einen beliebigen, gegebenen Punkt P "trifft". Hierbei ist der Berührpunkt zwischen Tangente und Schaubild nicht in jedem Fall bekannt. Der beliebige Punkt P kann je nach Aufgabenstellung auf dem Schaubild liegen oder daneben.

Wir beschreiben drei Verfahren, nach denen sich diese Aufgabentypen gelösen lassen.

Vergrößern

Tangentenprobleme in der gymn. Oberstufe als OpenOffice-Datei Download
Dokument als PDF Download

Lernvideo: Punkt-Steigungs-Form der Tangenten- und Normalengleichung

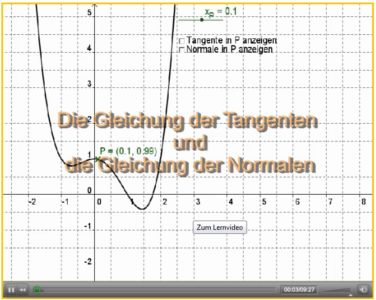
Die Punkt-Steigungsform der Tangenten- und Normalengleichung steht in jeder Formelsammlung. Die Darstellung kann leicht durch Verschiebung einer Ursprungsgeraden hergeleitet werden.
In einem Lernvideo wird dies vorgeführt. Den Film und die dabei gezeigten Animationen findest du unter dem nachfolgenden Link.

Zum Lernvideo zur Punkt-Steigungs-Form von Tangenten und Normalen

Modellierungsaufgaben:

Übungsaufgabe mit Animation und Lernvideo

Eine Gemeinde möchte eine Straße neu planen. Hierbei sind bestimmte Vorgaben zu beachten. Mathematisch lässt sich das Problem mit einer Tangentengleichung lösen - allerdings ist der Tangentenberührpunkt nicht gegeben (Tangentenproblem 2).
Im Lernvideo wird ein Lösungsweg ausführlich beschrieben. Zudem wird mit einer anspruchsvollen Zusatzfrage versucht, das Funktionsverständnis zu stärken.

Lernvideo und Animation zur Modellierung mit Tangenten

Weitere Übungsaufgabe mit ausführlicher Lösung

Am Beispiel einer Abituraufgabe werden die drei möglichen Lösungsverfahren beim zweiten Tangentenproblem angewandt (vgl. obiges Dokument).

Vergrößern

Abituraufgabe (Auszug) mit ausführlicher Lösung als OpenOffice-Datei Download
Dokument als PDF Download