Integralrechnung
Die Integralrechnung ist ein wesentlicher Bestandteil des Unterrichtsstoffs der gymnasialen Oberstufe.
Wir bieten Ihnen hier verschiedene Materialien sowohl für den Unterricht als auch zum Selbststudium oder zur Übung und Wiederholung.
Einführung der Integralrechnung
Auszug aus einem "Kultbuch"
Im Jahre 1938 veröffentlichte Alexander Niklitschek sein allgemein verständliches Buch "Im Zaubergarten der Mathematik", das bis heute in vielen Auflagen neu aufgelegt und in mehrere Sprachen übersetzt wurde. Das Buch hat mittlerweile "Kultstatus" erlangt. Die letzte Neufassung erschien 2001 als PDF-Ausgabe (3,1 MB).
Der folgende Auszug aus dem Kapitel über die Integralrechnung kann durchaus im Unterricht als Textvorlage dienen.

Textauszug zur Einführung der Integralrechnung als OpenOffice-Datei Download - Dokument als PDF Download
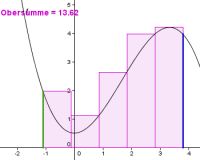
Zerlegungssummen als Näherung für das Integral einer Funktion
Das Integral einer (stetigen) Funktion f zwischen zwei Grenzen a und b wird über den Grenzwert einer Zerlegungssumme in diesem Intervall definiert. Die hier vorgestellte Animation verdeutlicht diese Näherung sowie Begriffe wie Obersumme und Untersumme. Neben der Zerlegung lassen sich auch die Intervallgrenzen sowie der Funktionsterm verändern. Mit Hilfe einer Fehlerrechnung können verschiedene Möglichkeiten für die Zerlegungssumme verglichen werden.
Rotationskörper
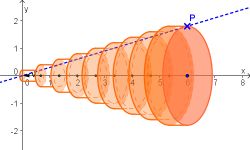
Mit einer Animation erkennen Sie hier anhand einer Ursprungsgeraden, wie Rotationskörper entstehen. Darüber hinaus finden Sie den Zusammenhang der Volumenintegralformel für Rotationskörper mit dem Integralbegriff (über Zerlegungssummen).
Einfache Aufgaben dienen zur Sicherung des Lernerfolges. Die Seite eignet sich für selbstständiges Lernen. Inhalte der Mittelstufe werden hierbei mit dem Formalismus der Integralrechnung vernetzt.
Lineare Substitution
Die Integration von zusammengesetzten Funktionen lässt sich nach einem einfachen Schema durchführen - allerdings nur, wenn die innere Funktion eine lineare Funktion ist.
Dieser Aufgabentyp ist eine beliebte Übung im Pflichtteil der Abitursprüfung.
Hier finden Sie eine Anleitung mit einem ausführlichen Beispiel sowie ein Übungsblatt mit Aufgaben und Lösungen zum "Abknicken" (Klapptest).
Sowohl die Anleitung zur linearen Substitution als auch das Aufgabenblatt liegen im PDF- und OpenOffice-Format vor, so dass sie es nach eigenen Wünschen verändern können. (Gerne veröffentlichen wir auch Ihre Aufgaben an dieser Stelle.)

Das Verfahren der linearen Substitution als OpenOffice-Datei Download
Dokument als PDF Download

17 Übungsaufgaben zur linearen Substitution mit Lösungen (Klapptest) als OpenOffice-Datei Download
Dokument als PDF Download



