Übersicht
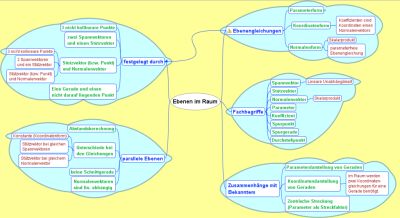
1. Mindmap Ebenen im Raum
Die folgende Mindmap wurde mit dem OpenSource-Programm FreeMind erstellt. Weitere Infos zu FreeMind
2. Lagebeziehungen bei Geraden und Ebenen
Welche unterschiedlichen Lagen können Geraden und Ebenen im Raum annehmen? Diese Fragestellung ist schon im Zusammenhang mit Geraden bekannt.
Auf den sehr gelungenen und gut strukturierten Seiten von Alexander Jung können Sie alles Wissenswerte über gegenseitige Lagen von Ebenen und Geraden nachlesen. Schöne Grafiken erleichtern hierbei das Verständnis.
zu den Seiten von Alexander Jung
Ausgewählte Aufgaben mit Lösungen zum Thema "windschiefe Geraden"
Die hier vorgestellten Arbeitsblätter eignen sich zur Vorbereitung auf Klausuren oder auf das Abitur. Es werden mögliche Fragestellungen mit zugehörigen Lösungsvorschlägen angeboten. Darüber hinaus ermöglichen Hinweise eine Vernetzung des Themas mit anderen Bereichen der analytischen Geometrie und der Analysis.
zu den Arbeitsblättern zum Thema "windschiefe Geraden"
3. Umrechnungen zwischen verschiedenen Darstellungsarten
Ebenen lassen sich auf verschiedene Arten beschreiben. Neben der Darstellung im Koordinatensystem spielen in der Schulmathematik die Parameterform, die Koordinatenform und die Hesse-Forme ein große Rolle. In vielen Fällen ist es hilfreich, wenn die Achsenabschnittsform als spezielle Art der Koordinatenform bekannt ist.
Von den Schülerinnen und Schülern der gymnasialen Oberstufe wird verlangt, dass sie die einzelnen Darstellungsarten ineinander überführen können.
In mehreren Musteraufgaben wird die Vorgehensweise ausführlich beschrieben.
(mit ausführlichen Lösungen)
4. Abstand Punkt - Ebene
Lernvideo 1: Abstandsberechnung Punkt-Ebene mit Bestimmung des Lotfußpunktes

In einem Lernvideo wird beschrieben, wie man mit einer Hilfsgeraden den Abstand eines Punktes zu einer Ebene berechnen kann. Hierfür muss der Lotfußpunkt bestimmt werden.
Das Verfahren in drei Schritten wird an einem Bespiel vorgeführt.
Lernvideo Teil 1: "Abstand Punkt Ebene mit Lotfußpunkt"
Lernvideo 2: Ebenenbestimmung mit vorgebenem Abstand

Falls bei einer Aufgabe der Abstand zu einem Punkt oder einer Ebene vorgegeben ist und zugehörige Ebenen gesucht werden, können verschiedene Fälle auftreten. Im zweiten Lernvideo zu Abständen von Ebenen wird hierauf ausführlich an einer Beispielaufgabe eingegangen.
Lernvideo 2: "Ebenenbestimmung mit vorgebenem Abstand"
Youtube-Lernvideo 3: Die Hessesche Normalform-Abstandsformel (HNF-Formel)
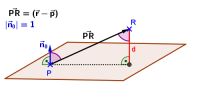
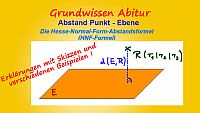
Warum lässt sich mit Hilfe der HNF-Formel der Abstand eines Punktes zu einer Ebene bestimmen? Warum benötigt man die Betragsstriche in der Formel? Antworten auf diese und weitere Fragen erhalten Sie anhand verschiedener Beispiele im Lernvideo. Zusätzlich unterstützt Sie ein Arbeitsblatt beim Verständnis.
Lernvideo 3 und Arbeitsblatt: Beweis der HNF-Formel mit Beispielen
5. Abstand Punkt - Gerade
Der Abstand zwischen einem Punkt und einer Geraden lässt sich auf verschiedene Arten berechnen. Unter dem folgenden Link finden Sie Anleitungen zu vier verschiedenen Lösungswegen.
Der erste Lösungsweg verwendet eine Hilfsebene und erklärt, wie diese bestimmt wird. Bei den anderen drei Techniken muss man zunächst eine Abstandsfunktion berechnen. Diese liefert beim Einsatz eines grafikfähigen Taschenrechners ein schnelles Ergebnis, führt mit einem Trick aber auch ohne Rechner zur Lösung.
6. Parallelität Ebene - Gerade
Wie lässt sich überprüfen, ob eine Gerade parallel zu einer Ebene verläuft? Bei diesem Aufgabentyp gibt es verschiedene Lösungsmöglichkeiten. Jede davon hat ihren Reiz.
Wie muss man einen Punkt verändern, dass die Verbindungsgerade durch einem anderen Punkt parallel zu einer gegebenen Ebene verläuft? Auch bei dieser Problemstellung gibt es verschiedene Lösungen.
Wir beschreiben für beide Fragestellungen je drei Lösungsmöglichkeiten in Form einer Musteraufgabe.