Das Skalarprodukt
Das Skalarprodukt spielt im Mathematikunterricht der Oberstufe eine zentrale Rolle. Es ermöglicht die Lösung vieler geometrischer Probleme ohne großen Rechenaufwand.
Mögliche Einführung des Skalarproduktes
Dieser Vorschlag zur Einführung des Skalarprodukts knüpft an die verallgemeinerte Aussage des Satzes von Pythagoras an. Da dieser Satz jedem Schüler ein Begriff ist, kann auch der anschauliche Kosinussatz (notfalls ohne Beweis) als Grundlage mitgeteilt werden.
Dokument als OpenOffice-Datei Download
Dokument als PDF Download
Zusammenstellung der Eigenschaften des Skalarproduktes (mit Rechenregeln)
Unmittelbar aus der Definition des Skalarproduktes ergeben sich verschiedene Eigenschaften.
Im folgenden Dokument sind diese Eigenschaften zusammengestellt.
Insbesondere die Anwendung der Rechenregeln spielen beim Beweisen eine zentrale Rolle. Dies wird einen Beispiel vorgeführt, wobei gezeigt wird, dass sich die Vektordarstellung und die Koordinatendarstellung des SKP entsprechen.
Dokument als OpenOffice-Datei Download
Dokument als PDF Download
Geometrische Interpretation des Skalarproduktes
Das Skalarprodukt lässt sich auf verschiedene Weisen geometrisch interpretieren.
Im folgenden Dokument beschreiben wir auf welche Art dies geschehen kann.
Die Kenntnis dieser Zusammenhänge kann neben geometrischen Anwendungen auch in besonderem Maß bei physikalischen Aufgabenstellungen hilfreich sein.
Dokument als OpenOffice-Datei Download
Dokument als PDF Download
Standard-Probleme für die Anwendung des Skalarproduktes
- Bestimmung des eingeschlossenen Winkels zwischen zwei Vektoren in der Ebene.
- Bestimmung des Winkels zwischen zwei Ebenen im Raum Schnittwinkel zwischen zwei Ebenen.
- Bestimmung des Winkels zwischen einer Ebene im Raum und einer Geraden Schnittwinkel zwischen einer Ebene und einer Geraden.
- Test auf Orthogonalität zweier Vektoren bzw. umgekehrt die Bestimmung von Parametern, so dass zwei Vektoren orthogonal sind.
- Bestimmund des Abstandes zweier paralleler Geraden im Raum z. B. für die Flächenberechnung von Parallogrammen.
- Bestimmung des Abstandes zweier windschiefer Geraden im Raum z. B. zur Überprüfung von Sicherheitsabständen bei Flugzeugrouten.
- Bestimmung des Abstandes zwischen einem Punkt und einer Ebene im Raum z. B. zur Berechnung einer Pyramidenhöhe.
- Bestimmung des Abstandes zwischen einem Punkt und einer Geraden im Raum z. B. zur Höhenbestimmung für die Flächenberechnung bei Dreiecken.
- Bestimmung eines Normalenvektors zu einer Ebene. Musteraufgabe .
- Aufstellen einer Normalengleichung für die Darstellung einer Ebene im Raum.
- Beweisen mit dem Skalarprodukt. Siehe Beweise in der Sekundarstufe 2 .
Anwendung in der Physik
Auch in der Physik spielt die Multiplikation von Vektoren eine große Rolle. Multipliziert man eine Kraftkomponente längs eines Weges mit der Länge eines Streckenvektors ergibt sich (bei Richtungsgleichheit) die längs dieses Weges aufgenommene Energie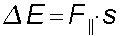 
. Mit dem Skalarprodukt erübrigt sich die Berechnung der Kraftkomponente in Wegrichtung, denn wegen 
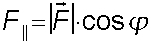folgt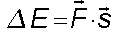 
.