Vektoren und lineare Unabhängikeit

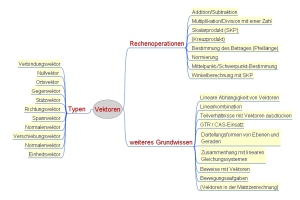
Vektoren

Vektoren spielen nicht nur in der Physik eine große Rolle. Bei linearen Gleichungssystemen treten sie beispielsweise als Lösungsvektor in Erscheinung. In der analytischen Geometrie lassen sich mit Vektoren Geraden und Ebenen beschreiben, sowie deren gegenseitige Lage untersuchen.

Bevor man auf diesem Gebiet einsteigt, sollte man sich die Zeit nehmen und sich mit den Grundbegriffen der Vektorrechnung auseinander setzten. In diesem Zusammenhang sei auf die sehr übersichtlich und verständlich gestalteten Seiten von www.mathe-online.at verwiesen. (Leider werden bei Verwendung des Modzilla-Browsers auf diesen Seiten Vektorpfeile und manche Klammern nicht korrekt angezeigt.)

Vergrößern

Hinweise:

• Lernen Sie die Vektordefinition auswendig.
• Verschaffen Sie sich zusätzlich eine Vorstellung von wichtigen Begriffen (Spitze, Schaft) sowie von speziellen Vektoren (Ortsvektor, Richtungsvektor, Verschiebungsvektor, Nullvektor).
• Arbeiten sie möglichst auch Unterschiede und Gemeinsamkeiten heraus.
• Mit Vektoren kann man auch rechnen. Da wir bisher nur mit Zahlen gerechnet haben, müssen wir für Vektoren unsere Rechenoperationen (Addition, Subtraktion, Multiplikation, Division) neu definieren. Auf diese Weise findet man beispielsweise für die Multiplikation drei verschiedene Varianten (Multiplikation mit einem Skalar, Skalarprodukt und Kreuzprodukt).

Das sollte man wissen:

• Im dreidimensionalen Raum ist ein Vektor durch ein geordnetes Zahlentripel eindeutig festgelegt.
• Man darf Vektoren beliebig im Raum verschieben - mit der Ausnahme von Ortsvektoren, deren Schaft immer im Koordinatenursprung liegt.
• Multipliziert man einen Vektor mit einer Zahl erhält man wieder einen Vektor. Diese Art von Multiplikation entspricht einer Streckung. Ist die Zahl negativ zeigt der gestreckte Vektor zusätzlich in die entgegengesetzte Richtung. Beim Skalar- und Kreuzprodukt werden hingegen zwei Vektoren miteinander multipliziert. Als Ergebnis ergibt sich beim Skalarprodukt eine Zahl, beim Kreuzprodukt hingegen ein Vektor.
• Addiert man die Quadrate der Vektorkomponenten, erhält man die Fläche des Quadrats mit der Vektorlänge als Seitenlänge. Die Wurzel dieser Summe entspricht somit der Vektorlänge - man spricht hierbei auch auch vom Betrag des Vektors.
• Das Kreuzprodukt kann man in der Oberstufenmathematik zur Bestimmung eines orthogonalen Vektors verwenden. Weiter erhält man aus dem Betrag des Kreuzprodukts den Flächeninhalt des von den beiden Vektoren aufgespannten Parallelogramms. Die Hälfte des Betrages ergibt folglich die Fläche des aufgespannten Dreiecks.
  Das Kreuzprodukt ergibt null, wenn entweder einer der Vektoren der Nullvektor ist (trivial) oder die beiden Vektoren parallel (linear abhängig) sind.
  Beachten Sie, dass die Rechnung hierbei recht fehleranfällig ist.