Einheiten beim Schwingungs- und Umdrehungsvorgang

Einheiten beim Schwingungs- und Umdrehungsvorgang.

Wenn es in der Akustik ans Rechnen geht, läßt für viele Schülerinnen und Schüler der Spaß an der Physik deutlich nach.

"Das mit den Einheiten kapiere ich nie!" hört man oft.
Dabei ist das gar nicht so schwer!

Von Pendeln und Rädern.

a)
Ein Pendel schwingt in einer Sekunde genau einmal hin und her. Die Zeit für eine Schwingung, die Schwingungs- oder Periodendauer T ist also 1 s.
Es macht dann in einer Sekunde genau eine Schwingung. Also ist die Frequenz f gerade 1 Schwingung je Sekunde.

b)
Ein Rad dreht sich in einer Sekunde genau einmal um die eigene Achse. Die Zeit für eine Umdrehung, die Umdrehungsdauer T, ist also 1 s.
Also ist die "Drehzahl" gerade 1 Umdrehung je Sekunde.

Wir suchen Gemeinsamkeiten:

Auch die Drehzahl eines Rades ist so etwas wie eine Frequenz f .
Die Frequenz gibt an, wieviele Schwingungen (Umdrehungen) das Pendel (Rad) in einer Sekunde ausführt.

Einheit der Frequenz:

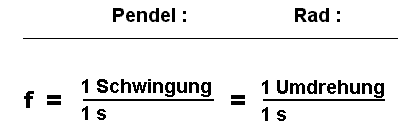Zur besseren Übersicht werden nun die Maßzahlen (grün) von den Einheiten (rot) getrennt. Die Sekunde "s" im Nenner in die Mitte gerückt.

Die Maßzahl wird vereinfacht.

Physiker sind bequem. Die Worte "Schwingung" und "Umdrehung" sind so lang. Machen wir sie kürzer!

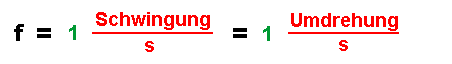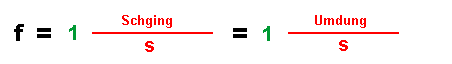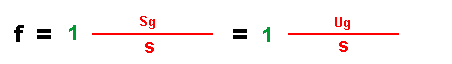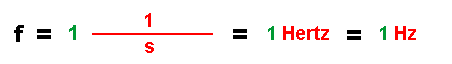Zuletzt steht bei der Einheit nur noch eine "1" im Zähler - sie ersetzt Worte wie "Schwingung" oder "Umdrehung". Diese "1" ist aber keine Maßzahl, sondern gehört zur Einheit, man kann sie daher auch nicht kürzen! Die Einheit "1/s" bekommt nun eine neuen Namen : ("Hertz" - nach Heinrich Hertz, einem berühmten Physiker) und eine Abkürzung ("Hz").

Zusammenhang Frequenz f und Periodendauer T.

Statt von "Schwingungsdauer" oder "Umdrehungsdauer" spricht man einfach von der Periodendauer T.

Auf einer anderen Seite wird erklärt wie Frequenz f und Periodendauer T miteinander zusammenhängen.
Von den Zahlen her sind beide einfach jeweils der Kehrwert des anderen.

Aber wie geht das mit den Einheiten??

Beispiel1:

Ein Rad an einem Motor benötigt für eine Umdrehung 20 ms. Mit welcher Umdrehungszahl (je Sekunde) dreht sich das Rad?

Rechne immer zuerst in die Grundeinheiten um - die Grundeinheit der Zeit ist die Sekunde!

Gegeben ist die Zeit für eine Umdrehung - also die Periodendauer T = 20 ms = 0,020 s. Gesucht ist die Umdrehungszahl je Sekunde - also die Frequenz f.

Es gilt:

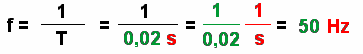
Hier wurden wieder Maßzahlen und Einheiten getrennt um das Prinzip deutlich zu machen.

Beispiel 2:

Eine Stimmgabel schwingt mit der Frequenz 440 Hz. Wie lange dauert ein Hin- und Herschwingen der Stimmgabelzinken?

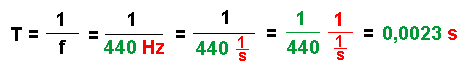
Diese Rechnung ist sehr ausführlich geraten um das Vorgehen zu verdeutlichen :

Aus der Einheit "Hz" wird - zum Rechnen - wieder "1/s".

Was für die Zahlen gilt, gilt dann auch für die Einheiten: "durch einen Bruch wird dividiert, indem man mit dem Kehrwert multipliziert."
So ergibt sich als Einheit wieder die Sekunde s.