Periodendauer und Frequenz beim Fadenpendel

Periodendauer und Frequenz beim Fadenpendel.

Bemerkung: Hier wurde die Fadenlänge nicht verändert, um nicht zu sehr zu verwirren. Um eine andere Frequenz und Periodendauer zu erreichen, müsste man die Fadenlänge ändern.

Betrachte die Schwingungsbewegungen am Besten so, dass die Zeit gerade startet (t = 0s), wenn das Pendel ganz links in der maximalen Auslenkung ist.

a)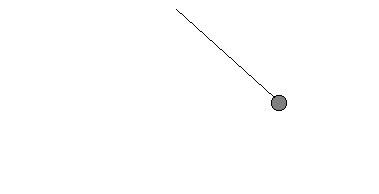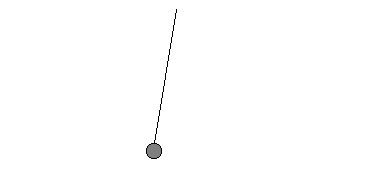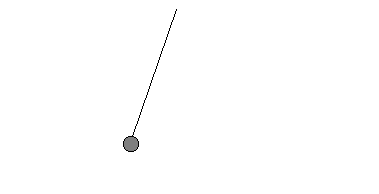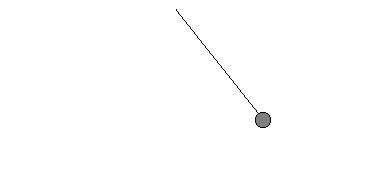	Dies ist ein sehr langsam schwingendes Pendel: von der maximalen Auslenkung links bis zur Mitte benötigt es etwa 1 s, bis zur maximalen Auslenkung rechts vergeht eine weitere Sekunde. Nach 3 s ist es wieder in der Mitte und nach 4 Sekunden erreicht es den Ausgangspunkt links. Danach beginnt der Pendelvorgang erneut, eine Periode ist zu Ende. Die Zeit für eine Periode nennt man die Periodendauer T. Die Periodendauer ist bei diesem Pendel T = 4 s. Die Zahl der Schwingungen in einer Sekunde bezeichnet man als Frequenz f. In einer Sekunde schafft dieses Pendel 1/4 seiner Pendelbewegung, seine Frequenz ist also f = 1/4 Hz..
b)	Was ist bei diesem Pendel anders? Es "schwingt schneller". Diesmal dauert es von ganz links nach ganz rechts nur 1 s, zurück wieder 1 s. Die Periodendauer ist hier also T = 2 s. In einer Sekunde schafft das Pendel also die Hälfte (1/2 ) seiner Pendelbewegung, seine Frequenz ist damit f = 1/2 Hz..
c)	Dieses Pendel ist ein "Sekundenpendel". Die Periodendauer ist hier also T = 1 s. In jeder Sekunde schafft das Pendel also genau eine (1) Pendelbewegung, die Frequenz ist damit f = 1 Hz.

Und wie ist es, wenn das Pendel noch "schneller schwingt", wenn es weniger als eine Sekunde für eine Schwingung benötigt?

d)
Benötigt das Pendel für eine Schwingung nur eine halbe Sekunde - ist also T = 1/2 s,
dann schafft es in einer Sekunde also zwei Schwingungen - die Frequenz ist damit f = 2 Hz.

e)
Ein Pendel, das für eine Schwingung nur T = 1/4 s benötigt, macht in einer Sekunde 4 Schwingungen, hat also die Frequenz f = 4 Hz.

Wir suchen einen Zusammenhang.

Je "schneller" also das Pendel schwingt, desto weniger Zeit benötigt es für eine Schwingung. Seine Periodendauer ist damit also klein.
Es schafft dann aber mehr Schwingungen in jeder Sekunde, seine Frequenz ist also groß.

Wir stellen unsere Ergebnisse einmal zusammen:

( Lässt man die Ergebnisse als Brüche stehen, sieht man den Zusammenhang besonders einfach. )

Betrachten wir die ersten beiden Zeilen der Tabelle (a) und b)) - und gehen von der Periodendauer T aus - so stellen wir fest:

Es gilt also: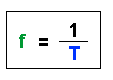

Wenn wir die letzten beiden Zeilen der Tabelle ansehen (d) und e)) und von der Frequenz f ausgehen, stellen wir fest, dass auch gilt:

oder in kurzer Formelschreibweise: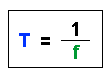

Damit haben wir den Zusammenhang zwischen Periodendauer T und Frequenz f gefunden.
Worauf du bei Einheiten achten mußt, erfährst du auf dieser Seite.