Der Compton-Effekt.

Wenn man die elektromagnetische Strahlung analysiert, die ein Raumgebiet durchdrungen hat, in der es freie Elektronen gibt, beobachtet man eine Streuung. Die Wellenlänge der gestreuten Strahlung hängt dabei von der Streurichtung ab.

Es seil die Wellenlänge der einfallenden Stahlung, und l’ die Wellenlänge der gestreuten Stahlung. Compton hat herausgefunden, dass die Differenz dieser beiden Wellenlängen ausschließlich von dem Streuwinkel q abhängt, und sich darstellen läßt als

wobei l_c eine Konstante mit dem Wert 2.4262 10^-12 m ist. (Compton-Wellenlänge)

Der Compton-Effekt erklärt sich als Wechselwirkung von elektromagnetischer Strahlung mit freien Elektronen, die wir zu Beginn als im Bezugssystem des Beobachters als ruhend annehmen wollen.

Physikalische Grundlagen.

Der Fotoeffkt hat gezeigt, dass das Photon eine Energie E=hf hat, und es hat auch einen linearen Impuls p=E / c

(Herr Franco Garcia benutzt statt W hier E für die Energie, es wurde beibehalten, um nicht alle Formeln ändern zu müssen, die meist als Grafiken realisiert sind).

Wenn man eine elektromagnetische Strahlung nicht nur als Welle sondern als Teilchenstrom versteht, dann haben die Photonen Impuls und Energie. Wenn wir die Wechselwirkung von elektromagnetischer Stahlung mit geladenen Teilchen beschreiben wollen, dann müssen wir die Gesetze des Energie- und Impulserhaltungssatzes benutzen.

Beim Photoeffekt brauchen wir den Impulserhaltungssatz nicht anzuwenden, weil das Elektron an ein Atom oder an ein Molekül gebunden ist.

Wir versuchen die Formel ausgehend von einem Stoß zwischen einem Photon und einem ruhenden Elektron zu erhalten.

1. Impulserhaltungssatz

• Es sei p der Impuls des einfallenden Photons,
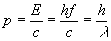
• und p' der Impuls des gestreuten Photons,
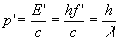
• und weiter p_e der Impuls des Elektrons nach dem Stoß, dann gilt vektoriell

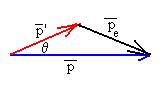p=p'+pe (1)

2. Energieerhaltungssatz

• Die Energie des einfallenden Photons ist E=hf .
• Die Energie des gestreuten Photons ist E’=hf ’ .
• Die kinetische Energie des Elektrons nach dem Stoß kann man beschreiben mitm_ev²/2. Da das gestoßene Elektron aber Geschwindigkeiten bekommt, die in der Größenordnung der Lichtgeschwindigkeit liegen, müssen wir den Energieausdruck durch die entsprechende relativistische Formel ersetzen:

darin ist m_e die Ruhemasse des Elektrons 9.1·10^-31 kg

Der Energieerhaltungssatz schreibt sich dann so:

(2)

Wenn wir die Gleichungen (1) und (2) benutzen, erhalten wir den wichtigen Ausdruck

Wenn wir noch den Zusammenhang zwischen der Frequenz und der Wellenlänge verwenden und die Gleichung umformen, bekommen wir den gleichwertigen Ausdruck:

Damit hängt der Ausdruck für die Propotionalitätskonstante l_c nur von den Naturkonstanten h, m_e und c ab. Man nennt l_c auch die Compton-Wellenlänge.

Damit haben wir herausgefunden, dass wir die Streung von elektromagnetsicher Strahlung an freien Elektronen als elastischen Stoß zwischen einem Photon und einem Elektron betrachten können, das im System des Beobachters in Ruhe ist.
Ausgehend vom Impuls- und Energieerhaltungssatz, sind wir zu einer Gleichung gekommen, die uns den Zusammenhang zwischen der Wellenlänge der einfallenden Strahlung l und der Wellenlänge der gestreuten Stahlung l’ und dem Streuwinkel q herstellen läßt.

Aktivitäten

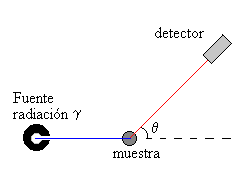In einem realen Experiment, ist der Detektor ein NaCl oder LiF Kristall, die Strahlungsquellela fuente ist ein Cs-137 Isotop, das einen scharfen Energiepeak bei 661.6 keV, was einer Wellenlänge von 1.878 10-12 m, (0.01878 A) entspricht.

Bei einem Schulexperiment wird meist eine Röntgenröhre als Quelle ( fuente) benutzt, der steuende Kristall (muestra) ist aus NaCL oder LiF und als Detektor verwendet man ein Geiger-Müller Zählrohr.

Mit Hilfe der Differenz zwischen den Wellenlängen der gestreuten Strahlung und der einfallenden Strahlung kann man die Compton-Wellenlänge l_C auch berechnen.
Ausgehend von dieser Konstante kann man weiterhin, wenn man die Naturkonstanten Lichtgeschwindigkeit c=3·10⁸ m/s und die Elektronenmasse m_e=9.1·10^-31 kg kennt, den Wert des planck'schen Wirkungsquantums bestimmen und erhält etwa 6.63·10^-34 Js.

Drücken Sie den Knopf mit Aufschrift Nuevo

• Ändern Sie den Winkel q des Detektors durch Ziehen mit der Maus,

Messen Sie die Wellenlänge der gestreuten Stahlung.

Beispiel:

Die Wellenlänge der im Winkel von 60 Grad gestreuten Strahlung ist l^'=0.03091 A. Berechnen Sie l_C und weiterhin, die planck'sche Konstante h.

0.03091A - 0.01878 A = l_C(1-cos60)
l_C=0.02426 A=2.426·10^-12 m = 2.4 pm

Im unteren Teil der Darstellung des Applets ist die Intensität der Gamma-Strahlung ,die der Detektor mißt, in Abhängigkeit von der Wellenlänge dargestellt. In dem interaktiven Programm sendet die Quelle elektromagnetische Strahlung aus, deren Wellenlänge im Mittel 0.01878 A = 1.87 pm beträgt. Die Form des "Peaks" bestimmt sich nach einer gaussschen Funktion :

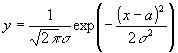
die um die Wellenlänge a, streut, und deren Wert s sich aus den Daten der Apparatur ergibt (Farbe blau). Die Strahlung, die der Detektor registriert, entspricht im Mittel einer anderen gaussschen Verteilung (Farbe rot) um die Wellenlänge der gestreuten Strahlung, deren Wert s mit dem Streuwinkel zunimmt.

Im unteren Teil des Applets sieht man die Werte der Wellenlängen der einfallenden und der gestreuten Strahlung in Angstöm (10^-10 m).
In wissenschaftlichen Abhandlungen über Atomphysik wird oft in dieser Einheit gerechnet. In der Schule bevorzugen wir Nanometer (1 nm = 10^-9 m) und Picometer (1 pm =10^-12 m).

Im rechten Teil des Applets können wir in animierter Form den elastischen Stoß zwischen einem Photon und einem ruhenden Elektron sehen. Wir können so grafisch verstehen, wie sich die Wellenlänge der gestreuten Strahlung mit dem Streuwinkel zunimmt.

Wir können auch sehen, wie das gestroßene Elektron einen Impuls p_e bekommt, und einen Winkel zur Einfallsrichtung des stoßenden Photons bekommt, den wir mit Hilfe des Impuls- und des Energieerhaltungssatzes berechnen können. Um damit die Geschwindigkeit v des Elektrons berechnen zu können, brauchen wir den relativistischen Ausdruck für den Elektronenimpuls

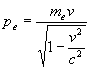
Ziehen Sie den Detektor mit der Maus um den Winkel zu ändern.

Adresse der Originalseite : http://www.sc.ehu.es/sbweb/fisica/cuantica/compton/Compton.htm

Appets: © Angel Franco Garcia - Universidad del Pais Vasco, Spanien;
Darstellung mit freundlicher Genehmigung des Autors.
deutsche Version : Grüninger, Landesbildungsserver