Elektronenbeugung - De Broglie-Beziehung.
1.) Lichtbeugung an einem Loch.
Lässt man Licht auf einen Einzelspalt fallen, so erhält man ein
Streifenmuster. (vgl. Seite zum Einfachspalt).
Was bekommt man, wenn man Licht auf ein kleines Loch fallen
lässt?
 | Man erhält sozusagen die Rotation eines Streifensystems, ein
Ringsystem. Dieses Interferenzsystem ist typisch für eine Welle. Bild: Beugung von rotem He-Ne-Laserlicht (632 nm) an einem Loch mit 0,25 mm Durchmesser |
2.) Licht als Teilchenstrahl.
Mit Licht kann man solche Interferenzexperimente am
Einzelspalt, Doppelspalt oder Gitter durchführen und man erhält die
bekannten Interferenzmuster, die man auch mit jeder anderen Wellenart bekommt.
Dadurch zeigt sich Licht als elektromagnetische Welle.
Charakteristische Größen einer Welle sind die Wellenlänge
λ und die Frequenz f.
Beim Fotoeffekt lernen wir Licht von einer anderen Seite
kennen:
dort besteht das Licht aus lauter definierten Energieportionen W = h
* f, die man Lichtquanten oder Photonen
nennt.
Das Licht verhält sich hier also eher wie ein
Teilchenstrahl.
Ähnlich wie ein Elektronenstrahl aus vielen Elektronen besteht, besteht
Licht aus einem Teilchenstrahl von vielen Photonen.
Photonen haben damit auch Teilcheneigenschaften wie Energie, Impuls und
sogar Masse.
3.) Auch Elektronen haben zwei Gesichter.
Elektronen sind Teilchen - sie haben eine Ladung, man kann sie beschleunigen
und bremsen wie "Bälle".
Aber sind wir uns sicher, dass Elektronen Teilchen sind?
Sind wir uns wirklich sicher?
Versuch:
Wir schießen Elektronen auf Grafitpulver in einem Anodenloch (vgl. Bild links) und beobachten auf einem
Leuchtschirm.
 |  |
| Grafitfolie in einem Loch in der Anode | Ringsystem der Elektronenbeugung |
Dort sehen wir ein Ringsystem, das genauso aussieht, wie das Ringsystem bei der Interferenz von Licht an einem Loch!
Vielleicht entsteht beim Aufprall der Elektronen auf dem Grafit ja
Licht, das dann diese Erscheinung hervorruft?
Halten wir aber einen Magneten in die Nähe, so erleben wir eine
Überraschung: das Ringsystem lässt sich ablenken!
Es kann sich also nicht um Licht handeln, denn Licht trägt keine Ladung
und kann daher im Magnetfeld nicht abgelenkt werden. Elektronen hingegen sehr
wohl.
Das Ringsystem wird also tatsächlich von Elektronen erzeugt!
Dies lässt nur einen Schluss zu:
Elektronen verhalten sich in diesem Experiment wie Wellen, sie haben
also - genau wie Photonen - nicht nur Teilcheneigenschaften sondern auch
Welleneigenschaften.
Ändert man die Anodenspannung der Röhre, so ändert sich der
Abstand der Ringe, genau wie beim Licht von unterschiedlichen
Wellenlängen.
Man kann also Elektronen auch eine Wellenlänge zuordnen, die von der
Anodenspannung abhängt.
Eine höhere Spannung Uc führt zu einer größeren Energie und damit zu einer größeren Frequenz - also einer kleineren Wellenlänge: das Ringsystem rückt enger zusammen (Herleitung weiter unten).
Leider ändert sich dabei auch die Intensität der Leuchterscheinung.
3.) Eine Ähnlichkeit wird ausgenutzt
Auf einer anderen Seite haben Sie die Beugung von Röntgenstrahlen an
einem Einkristall und die Braggsche Reflexionsbedingung kennen gelernt.
Röntgenstrahlung und Bragg
Beziehung
Die Anordnungen bei Röntgenbeugung und Elektronenbeugung sind sehr
ähnlich (vgl. Abbildungen)
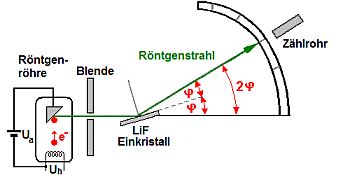
| Röntgenbeugung | Elektronenbeugung |
 |
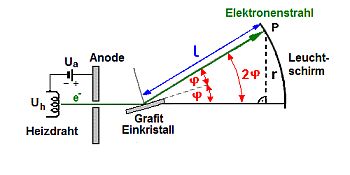 |
| Gemeinsamkeit: Die Anordnungen sind sehr ähnlich. In beiden Fällen wird eine elektromagnetische Welle an einem Kristall gebeugt. Die Winkelgeometrie ist identisch. |
|
| Unterschiede: In einer Röntgenröhre werden Elektronen von einer großen Spannung Ua auf eine Anode hin beschleunigt. Beim Aufprall auf die Anode entstehen die Röntgenstahlen erst. Die Beugung erfolgt an einem Salzkristall (z.B. LiF) Der Nachweis erfolgt in einem Geiger-Müller-Zählrohr. |
Unterschiede: Durch eine hohe Spannung werden Elektronenstahlen direkt erzeugt. Sie kommen (ähnlich wie bei einer Braunschen Röhre) direkt aus einer lochförmigen Anode. Die Beugung erfolgt an einem Grafit Kristall Der Nachweis erfolgt an einem Leuchtschirm. Die auftreffenden Elektronen bringen den Schirm an der Auftreffstelle zum Leuchten. |
Hier ist noch einmal das Bild der Elektronenbeugung dargestellt:
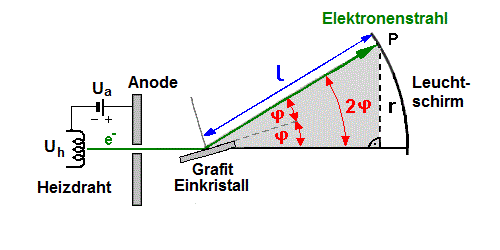
Im grau hinterlegten Dreieck gilt:

Wir hatten oben im Vergleich gesehen, wie ähnlich die Geometrie ist.
Bei der Röntgenbeugung (links) gilt für die Interferenz die Braggsche
Interferenzbedingung:
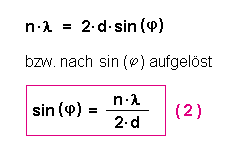
Wir können diese Ähnlichkeit nun weiter verwenden, indem wir die
beiden Sinusbeziehungen (1) und (2) gleichsetzen:
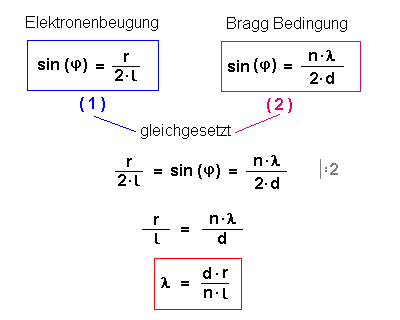
Auf diese Weise können wir die Wellenlänge der Elektronen ( für
eine Beschleunigungsspannung von 5 kV) ermitteln:
Dabei sind:
- r - Ringdurchmesser 1,1 cm
- l - Röhrendurchmesser 10 cm
- n - Ordnung ( hier n = 1 )
- d - Netzebenenabstand von Grafit (1,23 * 10-10 m)
Rechnet man dies aus, so kommt man auf eine Wellenlänge von etwa λ = 17 pm = 1,7 *10-11 m
4.) Umstieg vom Wellenbild ins Teilchenbild und umgekehrt - die de-Broglie-Beziehung.
Warum Licht und Elektronen sowohl Welleneigenschaften als auch
Teilcheneigenschaften haben, können wir nicht hier nicht klären.
Beide sind sogenannte Quantenobjekte.
Wir wären für den Anfang auch schon ganz zufrieden, wenn wir eine
Gleichung hätten, die uns einen einfachen Umstieg vom Wellenbild
ins Teilchenbild und umgekehrt gestattet.
Betrachten wir dazu Elektronen, die von einer Spannung von 5 kV beschleunigt wurden.
| Elektronen als Teilchen | Elektronen als Welle |
| Die Elektronen wurden von einer Spannung von U = 5 kV
beschleunigt. Damit haben sie die Energie W: 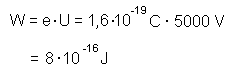 Daraus können wir ihre Geschwindigkeit v errechnen zu: 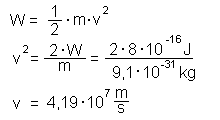 Den Elektronen können wir so einen Impuls p zuordnen: 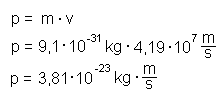 |
Aus der Auswertung des Elektronenbeugungsexperiments haben wir den Elektronen eine Wellenlänge von λ = 17 pm zugeordnet (s.o.) |
Wir wollen nun einmal die Einheiten sichten:
| Physikalische Größe: | Einheit: |
| Impuls p der Elektronen: | 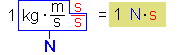 Impuls ist auch Kraftstoß oder "Schubs": eine Kraft wirkt eine bestimmte Zeit lang auf einen Körper ein |
| Wellenlänge λ der Elektronen: | 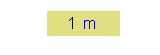 |
| Planck'sches Wirkungsquantum h: | 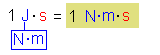 |
Die Einheiten legen folgende Vermutung nahe:
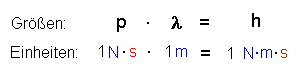
aber klappt das auch von den Zahlenwerten her?
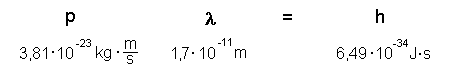
Die Vermutung ist bestätigt. Es gilt also:
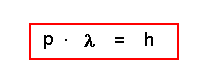
| Man nennt diese Beziehung die de Broglie-Beziehung ( Nobelpreis 1929 ) Die typische Teilchengröße Impuls p multipliziert mit der typischen Wellengröße λ ist gerade das Plancksche Wirkungsquantum h, das wir beim Fotoeffekt als Geradensteigung kennengelernt hatten. |
Mit Hilfe der de Broglie-Beziehung können wir nun einem
Elektron mit Impuls leicht eine Wellenlänge
zuordnen.
Ebenso kann man einem Photon einfach einen
Impuls und eine Masse zuweisen, wenn die
Wellenlänge bekannt ist.
Links zu Louis de-Broglie:
- Zu Louis de Broglie auf
Wikipedia
- Ein Interview mit
Louis de Broglie 1967 (französisch) YouTube
- Wie wird der Herr korrekt ausgesprochen?
Eine Französin muss es ja wohl wissen ;-)
Direkt finden Sie das hier:
Auch das ist eine gute Quelle hierzu (YouTube)
- Dass sich dabei viele Ausländer (insbesondere Amerikaner,
Engländer und Deutsche) damit schwer tun merkt man hier:
https://www.howtopronounce.com/louis-de-broglie/


