Röntgenstrahlen und Bragg Beziehung.

1.) Wie erzeugt man Röntgenstrahlen?

Im Jahre 1895 entdeckte Wilhelm Conrad Röntgen - angeblich eher zufällig - eine Art Strahlung, die er X-Strahlung nannte, die in vielen Ländern aber unter dem Namen Röntgenstrahlung bekannt ist. Er hatte mit Vakuumröhren und hoher Spannung experimentiert und dabei das Leuchten eines speziell beschichteten Papiers bemerkt.
Heute kennt man das "Röntgen" eher aus der Medizin: der Körper wird mit Röntgenstrahlung durchleuchtet. Knochen absorbieren dabei die Strahlung anders als das Zellgewebe, so kann man die Knochen sichtbar machen und zum Beispiel auf Brüche untersuchen.

Wie funktioniert eine Röntgenröhre?

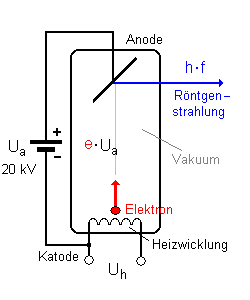Eine Röntgenröhre ist prinzipiell nicht anders aufgebaut als eine alte Radioröhre oder eine Fernsehbildröhre: aus einer Glühkathode werden Elektronen freigesetzt und von einer hohen Spannung Ua (etwa 20 kV) zu einer Anode hin beschleunigt. Prallen die Elektronen auf die Anode auf, so wird ihre kinetische Energie in elektromagnetische (Röntgen)strahlung umgewandelt. Dabei gilt: 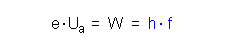Was hier passiert ist die Umkehrung des Fotoeffekts. Beim Fotoeffekt wird die Energie des Lichts (abzüglich der Ablöseenergie) in die kineteische Energie des Elektrons umgewandelt. Hier wird die kinetische Energie des Elektrons in die Energie der Strahlung umgewandelt. Siehe hierzu auch  fotoeffekt.htm

In der Röntgenröhre entsteht also elektromagnetische Strahlung der Frequenz f:

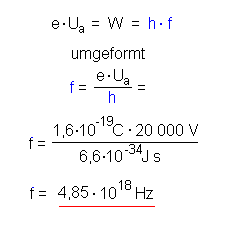
(zum Vergleich: sichtbares Licht 10¹⁴ Hz ).
Die Frequenz der Röntgenstahlung ist etwa 4 Zehnerpotenzen größer als die von Licht. Daher ist die Strahlung auch viel energiereicher (W = h * f).

Für die Wellenlänge λ bedeutet dies:

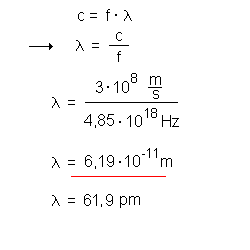
(zum Vergleich: sichtbares Licht 10^-7 m).

Wellenlänge λ und Frequenz f der entstehenden Strahlung hängen direkt von der Beschleunigungsspannung U_a ab (s.o.).
Je höher die Beschleunigungsspannung, desto höher ist die Frequenz f und damit die Energie der entstehenden Strahlung. Ab einer Spannung von 5 kV wird Röntgenstrahlung erzeugt.

Röntgengeräte, die mit dieser oder einer höheren Spannung betrieben werden, müssen in festen Zeitabständen vom TÜV überprüft werden - ähnlich wie ein Auto.
Auch alte Röhrenfernseher und -monitore wurden mit ähnlichen Anodenspannungen betrieben und erzeugen daher ebenfalls Röntgenstrahlung. Bei ihnen war eine gute Abschirmung der Röhrenoberfläche gegen Röntgenstrahlung - vor allem in den 80er und 90er Jahren - ein viel diskutiertes Thema.

2.) Sind Röntgenstrahlen elektromagnetische Wellen?

Wenn Röntgenstrahlen tatsächlich elektromagnetische Wellen sind, dann müsste man mit Ihnen auch all das machen können, was man auch mit Mikrowellen oder Licht machen kann - insbesondere Interferenzexperimente mit geeigneten Beugungsobjekten wie Doppelspalt oder Gitter.

Für den Abstand der k. Ordnung von der Mitte gilt bei einer Doppelspaltinterferenz folgende Gleichung (sofern die Winkel klein sind):


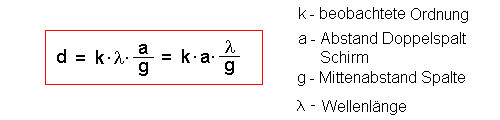
Vergleiche hierzu die Seite Interferenz beim Doppelspalt - Herleitung der Näherungsgleichung: fotoeffekt.htm

Welche Beugungsobjekte eignen sich zum Nachweis von Röntgenstrahlung?

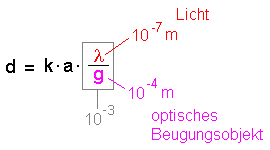
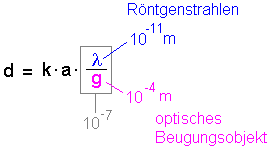
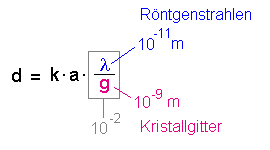
Optische Beugungsobjekte mit Licht beleuchtet	Optische Beugungsobjekte mit Röntgenstrahlenbeleuchtet	Kristallgitter mit Röntgenstrahlen beleuchet
Beim sichtbaren Licht sind die Wellenlängen λ in der Größenordnung von 10-7 m, der Doppelspaltabstand g in der Größenordnung 10-4 m. Der Faktor λ / g beträgt etwa 10-3 = 1/1000.	Lassen wir Röntgenstahlen mit einer Wellenlänge von 10-11 m auf ein solches Beugungsobjekt ( g = 0,1 mm = 10-4 m) treffen, dann ist der λ / g = 10-7 - damit wird d extrem klein. Die Interferenzerscheinung kann so nicht vernünftig beobachtet werden, weil die Ordnungen sehr eng zusammenrücken.	Da die Wellenlänge der Röntgenstrahlung ja fest liegt, kann man den Faktor λ / g nur dann groß bekommen, wenn man g sehr klein macht. Solche Beugungsobjekte sind optisch nicht herzustellen, kommen aber in der Natur als Salzkristalle vor (z.B. NaCl oder LiF). Bei ihnen ist der Abstand der einzelnen Atome etwa 10-9 m. Damit wird der Faktor λ / g dann wieder etwa 10-2, so dass man eine Interferenz beobachten kann.
gut geeignet	nicht geeignet	gut geeignet

Aufbau eines NaCl-Kristalls: Ein Kochsalzkristall (NaCl) hat einen würfelförmigen Aufbau. Die hell gefärbten Atome sind jeweils die Na Atome, die dunkel gefärbten Atome sind die Cl-Atome.

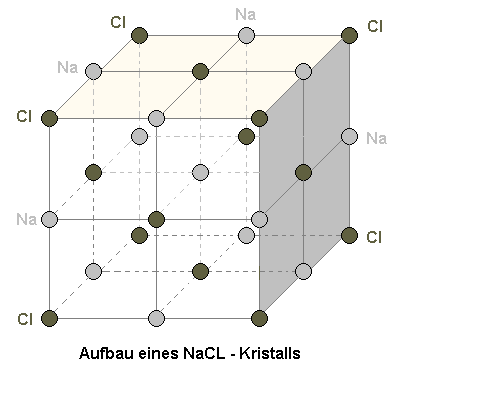3.) Reflexionsgesetz in der Ebene.

Sicher hast du erkannt, dass in diesem Modellversuch jeder Metallfleck für ein Atom steht. Die Styroporplatte ist sozusagen eine Atomlage eines Salzkristalls. Der ganze Kristall ist aus einzelnen Atomlagen aufgebaut, die man Netzebenen nennt. Jede Netzebene hat von der darüberliegenden Netzebene den Abstand d. Wenn wir meherer Styroporplatten zu einem "Sandwich" übereinander legen, haben wir ein Modell für den Salzkristall. Die Mikrowellenstrahlung kann das Styropor durchdringen und einen Metallfleck in einer anderen Ebene erreichen. Genauso kann auch die Röntgenstrahlung zum Beispiel die erste Netzebene durchdringen und ein Atom in der zweiten Netzebene treffen.

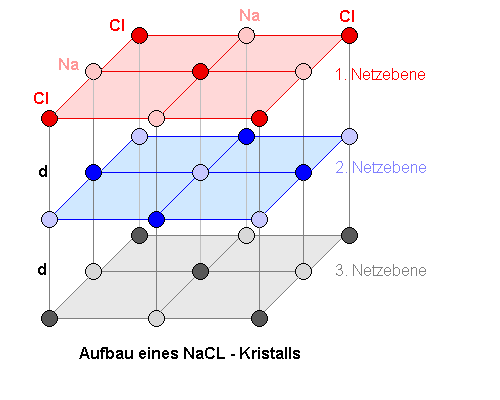4.) Reflexion und Interferenz im Raum - Bragg'sche Interferenzbedingung.

Klappt die Reflexion nun auch noch für jeden beliebigen Winkel? Eine dreidimensionale Betrachtung ist nicht nötig, es genügt, wenn wir die Interferenz an den vorderen Atomen des Kristalls betrachten. Wir lassen daher von den Netzebenen alles weg, was "nach hinten" in den Kristall hineingeht. Wir begnügen uns im Folgenden sogar nur mit den oberen beiden Netzebenen.

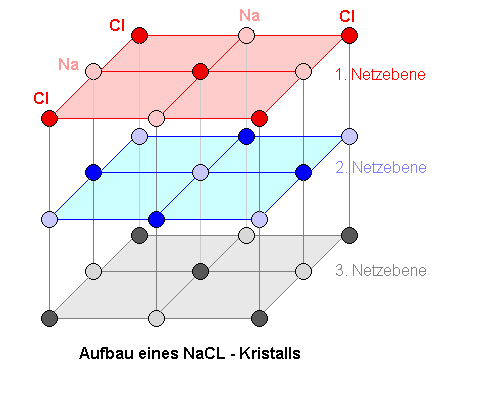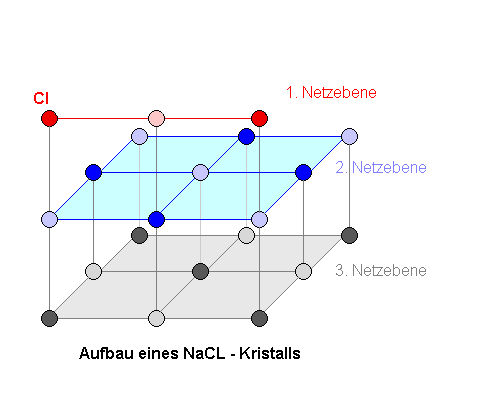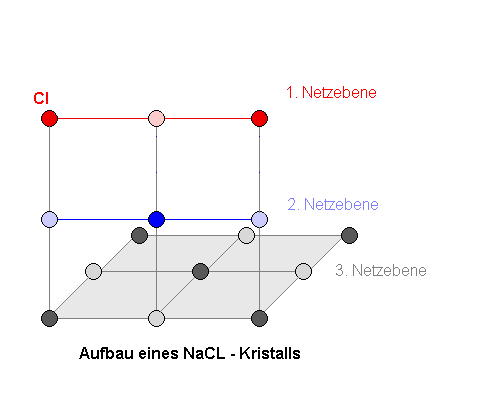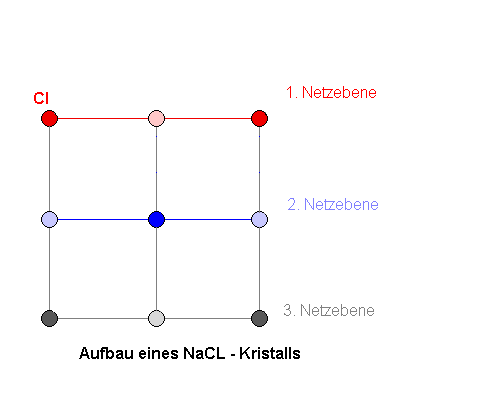
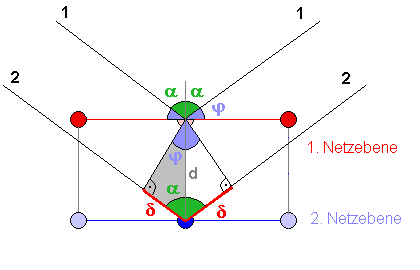Die Abbildung zeigt einen Schnitt durch die oberen zwei Netzebenen eines Kristalls. Es kommt nun zur Interferenz von Wellen, die an der obersten Schicht entstehen (1) , mit Wellen, die in der darunter liegenden Netzebene entstanden sind (2). Nur wenn diese konstruktiv interferieren, kann es unter dem entsprechenden Winkel zu Intensität kommen.

Im grau hinterlegten Dreieck gilt:


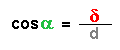
oder

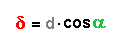
Der gesamte Gangunterschied δ_ges ist damit:

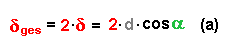
Statt Einfallswinkel und Ausfallswinkel zu verwenden, kann man die Beziehung auch mit dem sogenannten Glanzwinkel φ ausdrücken.
Dabei gilt:

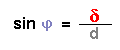
Im farbig hinterlegten Dreieck ist der obere Winkel ebenfalls dieser Glanzwinkel φ.
Die Winkelsumme im Dreieck ist 180°, an der linken Ecke ist ein rechter Winkel, also müssen die anderen beiden Winkel (grün und blau) zusammen 90° ergeben.
Damit gilt auch:

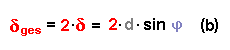
Man bekommt unter dem Winkel α ( bzw. φ) konstruktive Interferenz, also Verstärkung, wenn der gesamte Gangunterschied δ_ges gerade ein ganzzahliges Vielfaches der Wellenlänge λ ist.
Also gilt insgesamt:

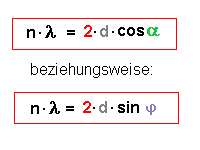Bragg'sche Interfenzbedingung

Diese Beziehungen nennt man nach ihren Enteckern die Bragg'sche Interferenzbedingung.
William Henry Bragg (1862 - 1942) und sein Sohn William Lawrence Bragg (1890 -1971) erhielten dafür 1915 den Physik-Nobelpreis.

Wikipedia: über die Bragg Bedingung

4.) Anwendung der Bragg'schen Bedingung.

Trifft Röntgenstrahlung also auf einen Einkristall aus mehreren Netzebenen, so bekommt man wegen der Bragg'schen Reflexionsbedingung nun nicht mehr unter jedem beliebigen Winkel ein Maximum sondern nur noch unter ganz bestimmten Winkeln.
Kennt man die Beschleunigungsspannung der Röhre, so ist die Wellenlänge λ damit bekannt. Man kann also durch Messung des Winkels den Netzebenenabstand des Kristalls bestimmen und so Kristalle untersuchen.
Umgekehrt kann man natürlich auch bei bekanntem Netzebenenabstand durch Messung der richtigen Winkel die Wellenlänge der Röntgenstrahlung ermitteln.

Es ging hier nur darum die Bragg'sche Bedingung plausibel zu machen und herzuleiten. Daher wurde die Idee etwas vereinfacht. In Wirklichkeit entsteht beim Aufprall der Elektronen auf die Anode nicht nur eine Wellenlänge sondern ein ganzes Spektrum (Röntgenbremsstrahlung) und man kann die Kristalluntersuchung auch mit polykristallinem Material statt eines Einkristalls durchführen (Debye-Scherrer-Verfahren).
Wikipedia: Debye-Scherrer-Verfahren

In der Kursstufe des Gymnasiums gehören diese Themen in Baden-Württemberg nicht zum Pfllichtprogramm.
Diese Seite dient auch nur dazu die Bragg'sche Bedingung bei der Röntgenbeugung herzuleiten.
Damit kann man ein Pflichtthema durch die Parallelität der Anordnungen leichter verstehen, die sogenannte Elektronenbeugung.
elektronenbeugung.htm