Vom "dicken" Draht zur Parallelschaltung von Widerständen.

1.) Ein einfacher Stromkreis.

Wir betrachten zunächst einen einfachen Stromkreis. Die Spannung möge 1 Volt betragen und der Widerstand im Stromkreis sei 1 Ohm. Dann beträgt die Stromstärke I = U / R = 1 A.

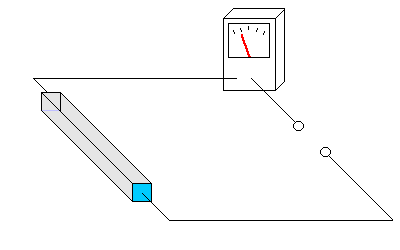
Abbildung 1

2.) Doppelte Fläche -> doppelte Stromstärke -> halber Widerstand.

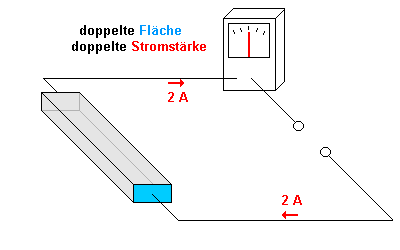
In der folgenden Grafik ist die Fläche genau doppelt so groß.
Um es geometrisch einfach zu machen, wurde sie als rechteckförmig angenommen.

In derselben Zeit strömen durch die doppelt so große Fläche doppelt so viele Elektronen - also ist auch die Stromstärke doppelt so groß.
Das bedeutet der Widerstand ist halb so groß wie in der Grafik weiter oben.
( R = U / I = 1 V / 2 A = 0,5 Ohm )

3.) Eine andere Betrachtungsweise: Doppelte Fläche = Parallelschalten von zwei Flächen.

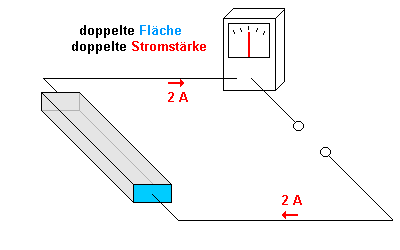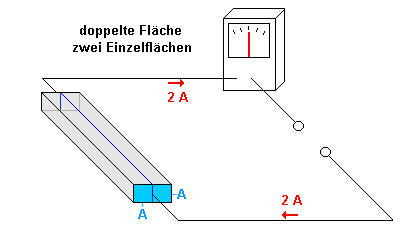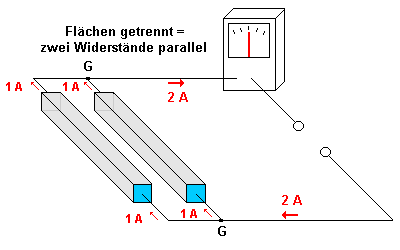
Die folgende Animation zeigt, dass man einen Widerstand mit doppelt so großer Fläche auch als Parallelschaltung von zwei Widerständen auffassen kann.
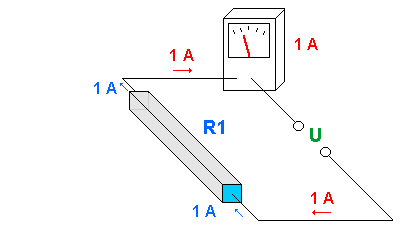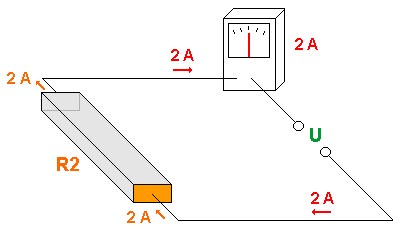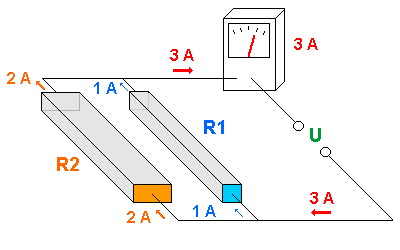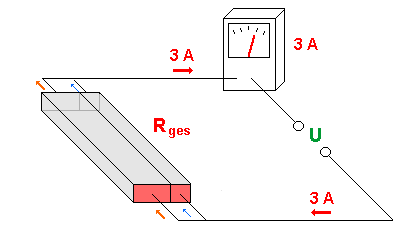
Beachte, dass die beiden Teilflächen lediglich getrennt werden. (Die Trennstelle ist zunächst blau markiert).
Die gesamte Fläche bleibt gleich groß. Die Stromstärke verändert sich ebenfalls nicht.

• Jeder der beiden Widerstände ist nun identisch mit dem Widerstand aus Abbildung 1, hat also einen Wert von 1 Ohm.
  
  
• Durch jeden der beiden (jetzt voneinander unabhängigen) Widerstände ergibt sich eine Stromstärke von 1 A.
  
  
• Da wir zwei Teilströme haben, die an den Punkten G zusammenfließen, ergibt sich eine Gesamtstromstärke von 2 A.
  
  
• Der gesamte Widerstand ist also nun R = U / I = 1 V / 2 A = 0,5 Ohm.

4.) Mehr Widerstände parallel, geringerer Gesamtwiderstand.

Um noch etwas mehr Erfahrung mit der Parallelschaltung zu sammeln, betrachten wir hier einen Draht mit der vierfachen Fläche im Vergleich zur Abbildung 1.
Die Animation zeigt wieder, dass man dies als Parallelschaltung von vier gleichen Widerständen auffassen kann.

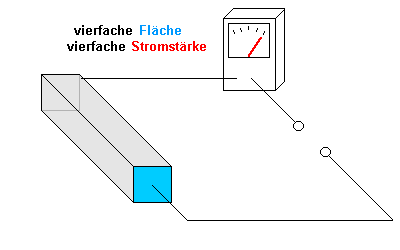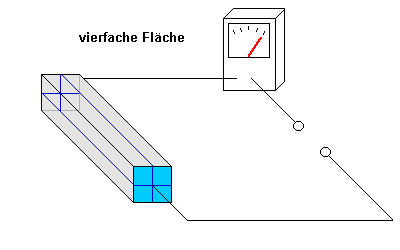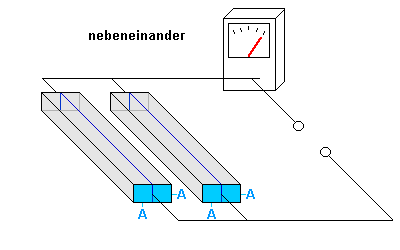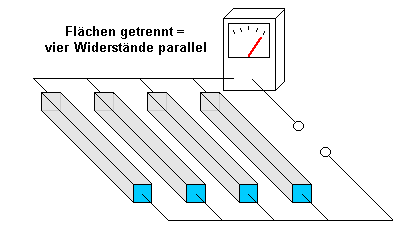
• Durch jeden der einzelnen Widerstände ergibt sich wieder eine Stromstärke von 1 A.
  
  
• Damit ergibt sich eine Gesamtstromstärke von 4 A.
  
  
• Der Gesamtwiderstand ist hier nun R = U / I = 1 V / 4 A = 0,25 Ohm.

5.) Unabhängig und doch gemeinsam .... der Weg zu einer Gleichung.

Wir beginnen nun eine allgemeine Gleichung für die Parallelschaltung zweier Widerstände zu erarbeiten.
Dabei gilt es folgende Dinge besonders zu beachten:

a) Beide Widerstände liegen an derselben Quelle -> an ihnen liegt die gleiche Spannung an.

Beide Widerstände liegen an derselben Quelle, an ihnen liegt also dieselbe Spannung U = 1,0 V an.
Bei jedem einzelnen Widerstand bestimmt sich also die Stromstärke durch den Widerstand mithilfe der Beziehung U = R * I bzw. I = U / R.
( unabhängig vom anderen Widerstand )

Für die Stromstärke im Widerstand R1 gilt: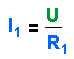
Für die Stromstärke im Widerstand R2 gilt: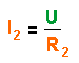

b) Addition der einzelnen Stromstärken zur Gesamtstromstärke (2. Kirchhoff-Gesetz).

• Die beiden Widerstände sind unabhängig voneinander.
  Der Stromfluss durch jeden einzelnen von ihnen hängt nicht davon ab, ob der andere Widerstand im Stromkreis ist oder nicht.

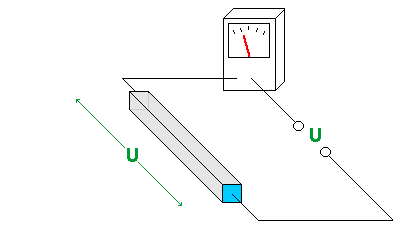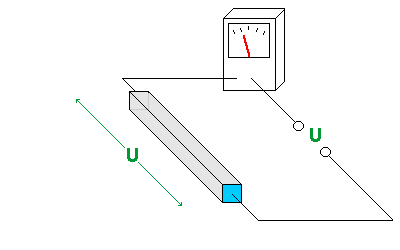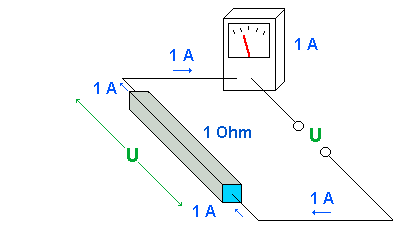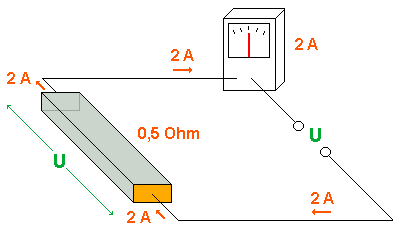
Beachte in der Animation besonders die Stromstärken und auch die Anzeige des Messinstruments für die Gesamtstromstärke.

Die Gesamtstromstärke ist damit :

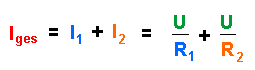
Dieselbe Stromstärke erhält man auch, wenn man statt der zwei Widerstände R₁ und R₂ nur einen Widerstand R_ges im Stromkreis hätte.
Man nennt diesen dann auch den Gesamtwiderstand oder Ersatzwiderstand.

Es gilt also auch:

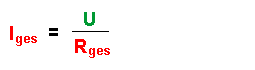
Links steht jeweils die Gesamtstromstärke I_ges. Setzt man die beiden Formeln gleich so erhält man:

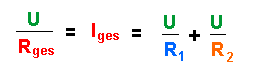
Kürzt man noch mit U, dann erhält man die allgemeine Gleichung für einen Widerstand, der zwei parallel geschaltete Widerstände ersetzen kann:

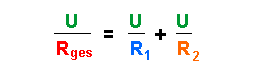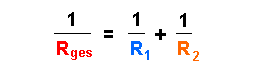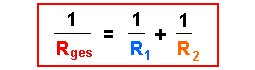
6. Noch ein Beispiel zum Schluß.......

Beispiel:

Mit welchem Widerstand kann man zwei parallelgeschaltete Widerstände von 100 Ohm und 50 Ohm ersetzen?

Gegeben : R₁ = 50 Ohm ; R₂ = 100 Ohm.
Gesucht : R_ges

Lösung:

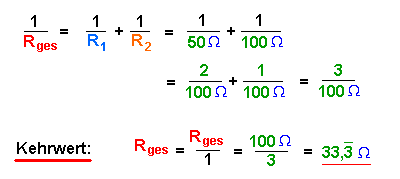
Um es deutlich zu machen, wurde hier die Zahlenrechnung farblich von der Einheit unterschieden.

Besonders einfach rechnet man hier mit Brüchen. Erweitere geeignet auf den Hauptnenner.
Vergiss unter keinen Umständen den Kehrwert zu bilden, wenn du den Ersatzwiderstand berechnen willst!

Grüninger, Landesbildungsserver Baden-Württemberg