Die Parallelschaltung (virtuelles Labor)

Diese Seite ist nicht als Ersatz für ein Realexperiment oder ein Praktikum zu diesem Thema gedacht. Gerade bei diesem Thema ist eigenes Handeln und Erfahren der Schülerinnen und Schüler unverzichtbar. Die Seite kann aber dazu dienen sich die Theorie der Parallelschaltung zu erarbeiten, eigene Messwerte aus dem Praktikum zu überprüfen, oder das Gelernte Zuhause noch einmal zu wiederholen und zu vertiefen. Das nebenstehende Foto zeigt einen möglichen Praktikumsaufbau. Das Netzgerät links ist auf dem Bild nicht zu sehen. Die Verknüpfungspunkte sind hier mit Steckhülsen ausgeführt. Die Beschriftung bezieht sich auf das Java-Applet im linken Fenster.

Fragen und Aufgaben:

1.) Grundlagen der Parallelschaltung.

Schaue Dir mit den Grundeinstellungen zunächst die linke Seite (Zwei Widerstände parallel) an.

• Welche Spannung liegt an den beiden Widerständen R₁ und R₂ an?

Setze nun das Kontrollhäkchen oberhalb des linken Fensters bei "Stromwege".

• Welche Wege können die Elektronen am Punkt A nehmen?
• Was geschieht im Punkt B?
• Was bestimmt, wie groß die Stromstärken im blauen und im roten Zweig sind?

Nach oben zum Applet.

2.) Zusammenhang Widerstände R₁ und R₂ und Teilströme I₁ und I₂

• Was kann man über die beiden Stromstärken I₁ und I₂ aussagen, wenn die beiden Widerstände gleich groß sind?
  (Versuche z.B. auch 20 Ohm und 20 Ohm oder 50 Ohm und 50 Ohm)

• Wo ergibt sich die größere Stromstärke?
• Wo ergibt sich die kleinere Stromstärke?
• Kannst Du die beiden Stromstärken in den Teilkreisen auch berechnen?
  Probiere Deine Idee hierzu aus und vergleiche mit dem Ergebnis in der Simulation!

Nach oben zum Applet.

3.) Einzelstromstärken und Gesamtstromstärke.

Sieh' Dir die Einzelstromstärken I₁ und I₂und die Gesamtstromstärke I_ges an.
Probiere verschiedene Widerstandskombinationen aus.

• Welchen Zusammenhang zwischen den drei Stromstärken kann man feststellen?

Nach oben zum Applet.

4.) Ein Widerstand, der beide Widerstände ersetzen kann, wird gesucht.

Man nennt diesen einen Widerstand den Gesamtwiderstand oder auch Ersatzwiderstand.

Wähle im linken Fenster die beiden Widerstände R₁ und R₂ mit jeweils 10 Ohm aus (Beide Widerstände haben gleiche Werte).

• Wie groß muss der Gesamtwiderstand (rechtes Fenster) gewählt werden?
• Welchen Zusammenhang kannst Du vermuten?
• Probiere Deine Vermutung nun auch für 20 Ohm und 20 Ohm bzw. 50 Ohm und 50 Ohm aus!

Wähle nun für R₁ und R₂ 20 Ohm und 10 Ohm aus.

• Wie groß ist der Gesamtwiderstand nun (durch Probieren finden)?
• Vergleiche den Wert des Gesamtwiderstandes mit den Werten von R₁ und R₂!
  Was kann man feststellen?
  
• Gilt dies auch für andere Kombinationen von verschiedenen Widerständen R₁ und R₂ ?

Nach oben zum Applet.

4.) Ein wenig Theorie kann nie schaden ...

Wahrscheinlich hast Du bei Deinen virtuellen Experimenten von oben folgendes herausgefunden:

• Die beiden Widerstände R₁ und R₂ liegen beide an derselben Spannung U, der Spannung der Quelle.
  Teilspannungen gibt es bei der Parallelschaltung nicht. (Ergebnis aus 1.))
  
  
  
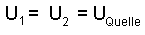
• Der Gesamtstrom teilt sich auf zwei Stromwege auf.
  Im Punkt A kann ein Elektron entweder den "blauen" Weg durch den Widerstand R₁ wählen oder den "roten" Weg durch den Widerstand R₂.
  Bei B vereinigen sich diese Stromwege wieder.
  Weil keine Ladung verloren geht, ist die Gesamtstromstärke I_ges die Summe der Einzelstromstärken I₁ und I₂.
  
  Also gilt:
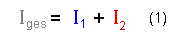  (Gesetz von Kirchhoff )
  
  
• Wie groß die Stromstärke im einzelnen Teilzweig ist, hängt vom Widerstand in diesem Zweig ab.
  Ist der Widerstand dort groß, ist die Stromstärke klein und umgekehrt. (Ergebnis aus 2.))
  
  Dabei gilt:
  
  
  
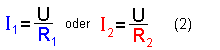
• Im rechten Fenster ergibt sich zwischen der Spannung U und der Gesamtstromstärke I_ges folgender Zusammenhang:
  

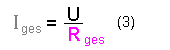
Setzt man nun die Zusammenhänge (2) und (3) in die Gleichung (1) ein, so ergibt sich:

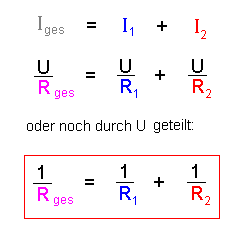
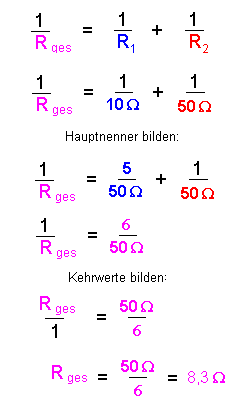
Zum Schluss zum besseren Verständnis noch ein Rechenbeispiel (rechts): Zwei Widerstände von 10 Ohm und 50 Ohm werden parallel geschaltet. Welchen Wert muss ein Widerstand haben, der beide Widerstände ersetzen kann? Schaue Dir die Rechnung genau an. Gehe dann in die Simulation von oben und wähle die beiden Widerstände mit zu 10 Ohm und zu 50 Ohm aus. Gib bei Gesamtwiderstand 8,33 Ohm ein. Überzeuge dich davon, dass dann in beiden Fenstern die Gesamtstromstärke gleich groß ist. Wähle eine andere Widerstandskombination aus. Berechne nach dem Beispiel rechts den Gesamtwiderstand dieser Kombination. Prüfe das Ergebnis in der Simulation oben nach.

Nach oben zum Applet.

Die Simulationen entstanden mit Hilfe von Physlets von Wolfgang Christian und Mario Belloni vom Davidson College, USA ( Copyright Hinweise) © Javascript dieses Problems, Fotos, Grafiken und Seite: Klaus-Dieter Grüninger, Landesbildungsserver Baden-Württemberg, 2008