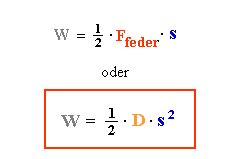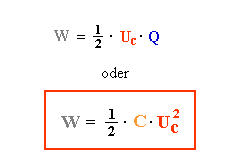Energie einer Feder - Energie eines Kondensators |
| Man kann in die bewegten Grafiken klicken und sie im
Einzelbildmodus weiterschalten. |
(1) Immer diese Gleichgewichte!
Spannen einer Feder |
Laden eines Kondensators |
| Zuerst ist die Feder ungespannt. |
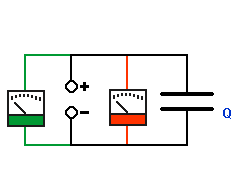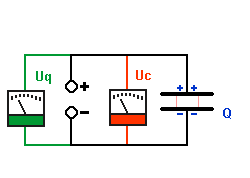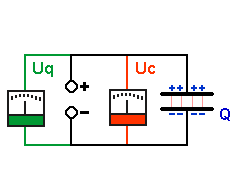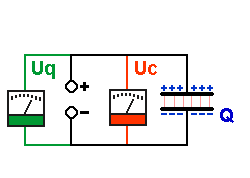
Zuerst ist der Kondensator ungeladen. |
| Am Anfang ist es einfach die Feder zu spannen. Je weiter die Feder gespannt wird (Spannstrecke s), um so schwerer ist es, sie weiter zu spannen, weil die Federkraft dem entgegenwirkt. |
Am Anfang ist es einfach Ladungen auf den Plattenkondensator zu bringen. Je mehr Ladungen schon auf den Kondensatorplatten sind (Ladung Q), um so schwerer ist es, weitere Ladungen darauf zu bringen, weil sich gleichnamige Ladungen abstoßen. |
 |
 |
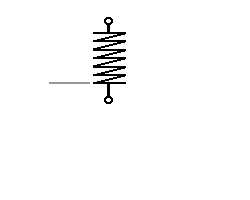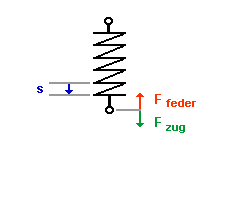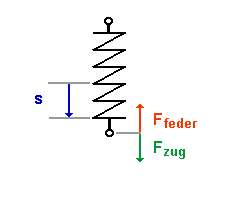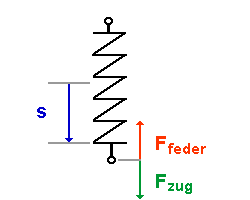
| Je größer die Spannstrecke s, desto mehr nimmt die Federkraft Ffeder zu. Also ist die Federkraft Ffeder stets gleich der Zugkraft Fzug |
Je mehr Ladungen auf den Platten sind,
desto größer wird die Spannung am Kondensator
Uc. Also ist die Spannung an den Anschlüssen des
Kondensators Uc stets gleich der Spannung der Quelle Uq. |
| Es herrscht ein
Kräftegleichgewicht. |
Es herrscht ein
Spannungsgleichgewicht. |
(2) Zwei Gesetze, die sich ähnlich sind.
| Für den Zusammenhang
zwischen der Federverlängerung s und der
Federkraft Ffeder gilt das
Hooke'sche Gesetz: Dabei ist D, die Federhärte die Kenngröße der Feder. |
Für den Zusammenhang zwischen der
Ladung auf dem Kondensator Q und der
Spannung an seinen Platten Uc gilt das
Kondensatorgesetz: Dabei ist C, die Kapazität, die Kenngröße des Kondensators. |
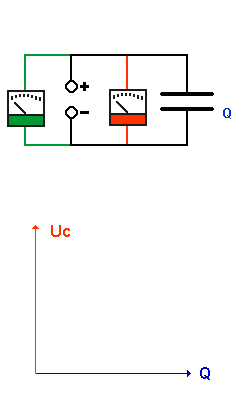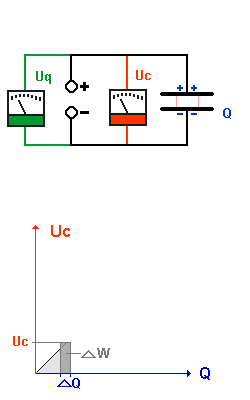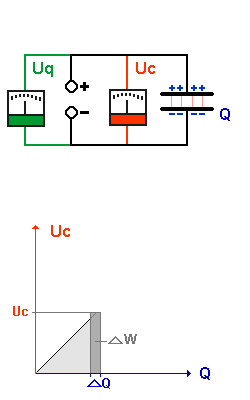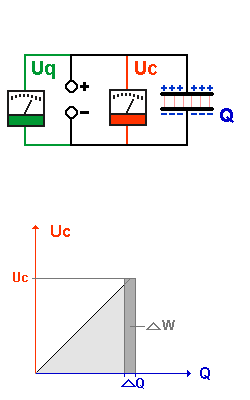
| (3) | Wie sehen die zugehörigen Diagramme aus? |
| Welche Arbeit muß beim Spannen / Laden verrichtet werden? |
| Da Ffeder proportional s, ist das Ffeder(s)-Diagramm einer Feder eine Ursprungsgerade. |
Da Uc proportional Q, ist das Uc(Q)-Diagramm eines Kondensators eine Ursprungsgerade. |
||||
|
 |
||||
 |
 |
||||
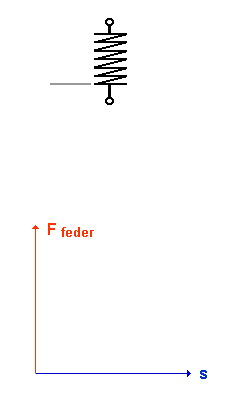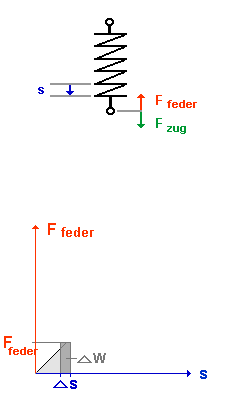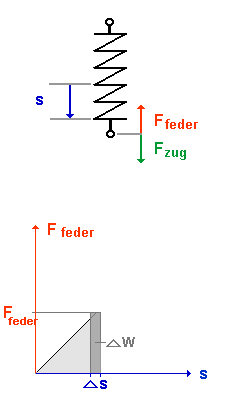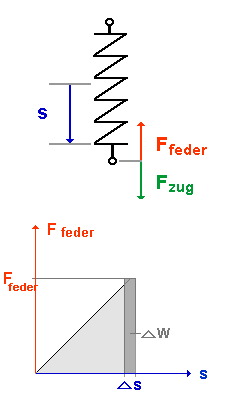
| Diese Arbeit muß um so größer sein, je weiter die Feder schon gespannt ist und je größer die Federkraft Ffeder damit wird. |
Diese Arbeit muß um so größer sein, je mehr Ladung schon auf den Platten ist und je größer die Kondensatorspannung Uc damit wird. |
||||
| Die gesamte Arbeit, die man zum Spannen der Feder aufbringen muß, ist die Fläche unter der Kurve 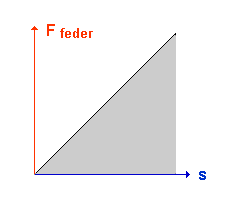
|
Die gesamte Arbeit, die man zum Laden des Kondensators aufbringen muß, ist die Fläche unter der Kurve 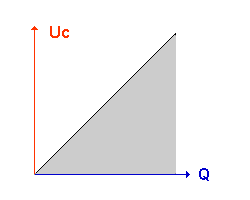
|
||||
|
|
© Grüninger, Landesbildungsserver