Messung der elektrischen Feldstärke mit einer Probekugel.

1.) Das Realexperiment zum elektrischen Feld im Plattenkondensator.

Um zu untersuchen, wie man die Stärke des elektrischen Feldes zwischen zwei Kondensatorplatten definieren kann, wird eine kleine Kugel an einem Nylonfaden isoliert aufgehängt. Sie trägt eine positive Probleladung q. Wird eine Spannung an die Kondensatorplatten angelegt, entsteht zwischen den Platten ein homogenes, elektrisches Feld. Die Kugel wird durch die elektrische Kraft Fel nach rechts ausgelenkt. Eine Teilkomponente der Gewichtskraft (die Rückstellkraft FR) wirkt dieser auslenkenden Kraft entgegen. Die Kugel wird so weit ausgelenkt, bis Rückstellkraft und elektrische Kraft gleich groß sind.

2.) Theoretische Betrachtung: Kräfteverhältnisse an der geladenen Kugel.

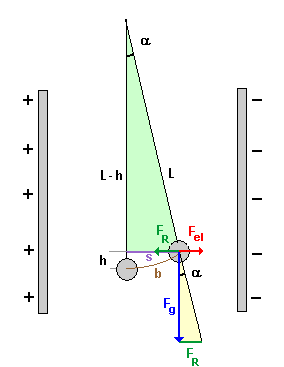Hier ist die Situation aus dem Foto von oben noch einmal schematisch dargestellt. Die Kugel ist wie ein Pendel aufgehängt. In Wirklichkeit ist der Winkel Alpha natürlich viel kleiner als hier gezeichnet. Bei realen Experimenten beträgt er deutlich weniger als 5 Grad! Für kleine Auslenkwinkel Alpha kann man folgende Näherungen machen: Die Länge des Kreisbogens b ist etwa gleich der Auslenkstrecke s. Die Rückstellkraft FR, die eigentlich tangential an den Kreisbogen b verläuft, kann horizontal in Richtung der Strecke s angenommen werden. Der Sinus des Auslenkwinkels ist etwa gleich dem Tangens des Auslenkwinkels.

Probiere die letzte Näherung einfach mit dem Taschenrechner aus:
bei Winkeln kleiner 5 Grad unterscheiden sich der Sinus und der Tangens eines Winkels praktisch nicht!

Im hellgrünen Auslenkungs-Dreieck gilt (s ist die Gegenkathete, l die Hypothenuse):

Im hellgelben Kräfte-Dreieck gilt (F_R ist der Gegenkathete, F_g die Ankathete):

Mit der Näherung Sinus des Winkels = Tangens des Winkels folgt:

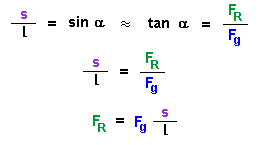
Die Gewichtskraft der Kugel F_g und die Pendellänge l sind konstant. Damit ist also die Rückstellkraft F_R (für kleine Winkel) der Auslenkung s proportional (vgl. letzte Zeile der Gleichungen oben)
Weil ja in einer festen Auslenkposition die Rückstellkraft F_R und die elektrische Kraft F_el gleich groß sind, sind auch die Auslenkung s und die elektrische Feldkraft F_el proportional.

3.) Doppelte Ladung - doppelte Kraft.

a) Man legt eine Spannung an die Kondensatorplatten an. Die Auslenkung s der Kugel wird markiert.

Nun berührt man die geladene Pendelkugel (1) mit einer gleichen, zweiten Kugel (2), die ungeladen ist. Die Ladung der Pendelkugel verteilt sich dabei gleichmäßig auf beide Kugeln, so daß die Pendelkugel (1) anschließend nun noch die halbe Ladungsmenge q trägt.

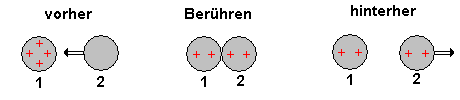
Nun wird die Pendelkugel nur noch um die halbe Strecke s ausgelenkt, also wirkt nur noch eine halb so große elektrische Kraft Fel auf sie.

Legt man eine kleinere Spannung an die Platten an, so wird die Auslenkung der Pendelkugel kleiner. Wenn man die Ladung q auf der Pendelkugel wieder halbiert, so halbiert sich auch hier die Auslenkung.

4.) Die angelegte Spannung bestimmt die Feldstärke.

Hält man die Ladung auf der Pendelkugel konstant und verändert die Spannung U an den Kondensatorplatten, so ändert sich die Auslenkung der Pendelkugel.
Bei doppelter Spannung U ergibt sich auch die doppelte Auslenkung s. Also ist auch die elektrische Kraft F_el der Spannung U proportional. Weil die Ladungsmenge q konstant ist, ergibt sich damit auch die doppelte elektrische Feldstärke E.

5.) Auch der Plattenabstand spielt eine Rolle.

Schiebt man bei konstanter Spannung die Kondensatorplatten näher zusammen, so vergrößert sich die Auslenkung s.
Bei halbiertem Plattenabstand d ergibt sich die doppelte Auslenkung s und damit doppelte el. Feldkraft F_el bzw. die doppelte elektrische Feldstärke E.

Spiele die Zusammenhänge noch einmal in einem virtuellen Experiment durch.
Die hier hergeleiteten Zusammenhänge sind Grundlage für die Simulation.